![\[\begin{tabular}{|l|l|l|l|l|l|} \hline Size & 20 & 21 & 22 & 23 & 24 \\ \hline Frequency & 6 & 4 & 5 & 1 & 4 \\ \hline \end{tabular}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-67012859a1da859a3d725cf996f07cf6_l3.png "Rendered by QuickLaTeX.com")
Solution:
Data distribution is given
We now need to find the mean deviation about the mean of the distribution.
Draw a table of the data given.
![\[\begin{tabular}{|l|l|l|} \hline Size $\left(x_{i}\right)$ & Frequency $\left(f_{i}\right)$ & $f_{i} x_{i}$ \\ \hline 20 & 6 & $20 \times 6=120$ \\ \hline 21 & 4 & $21 \times 4=84$ \\ \hline 22 & 5 & $22 \times 5=110$ \\ \hline 23 & 1 & $23 \times 1=23$ \\ \hline 24 & 4 & $24 \times 4=96$ \\ \hline Total & 20 & 433 \\ \hline \end{tabular}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-e47f0191816d64dbe9f037d4b79f17d6_l3.png "Rendered by QuickLaTeX.com")
It is known that mean, 
In order to find the mean deviation we need to construct another table
![\[\begin{tabular}{|l|l|l|l|l|} \hline Size $\left(\mathrm{x}_{\mathrm{i}}\right)$ & Frequency $\left(\mathrm{f}_{\mathrm{i}}\right)$ & $\mathrm{f}_{\mathrm{i}} \mathrm{x}_{\mathrm{i}}$ & $\mathrm{d}_{\mathrm{i}}=\mid \mathrm{x}_{\mathrm{i}}-$ mean $\mid$ & $\mathrm{f}_{\mathrm{i}} \mathrm{d}_{\mathrm{i}}$ \\ \hline 20 & 6 & 120 & $1.65$ & $9.90$ \\ \hline 21 & 4 & 84 & $0.65$ & $2.60$ \\ \hline 22 & 5 & 110 & $0.35$ & $1.75$ \\ \hline 23 & 1 & 23 & $1.35$ & $1.35$ \\ \hline 24 & 4 & 96 & $2.35$ & $9.40$ \\ \hline Total & 20 & 433 & $6.35$ & $25.00$ \\ \hline \end{tabular}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-17a311ffd0ebb92e24dc5e0bf56a29c3_l3.png "Rendered by QuickLaTeX.com")
Therefore, Mean Deviation becomes,
M.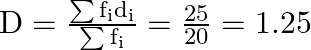 
As a result, 
is the mean deviation about the mean of the distribution.