Solution:
(i) ![]() to
to ![]() terms.
terms.
Let’s take 5 as a common term therefore we obtain,
![]() terms
terms ![]()
Now multiplying and dividing by 9 we obtain,
![]() terms
terms ![]()
![]() terms
terms ![]()
![]()
Therefore the G.P is
![]()
Using the formula,
The sum of GP for ![]() terms
terms ![]()
Where, ![]()
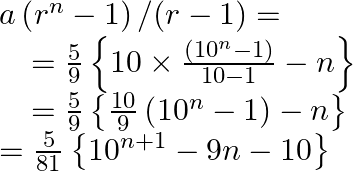
(ii) ![]() to
to ![]() terms.
terms.
Let’s take 7 as a common term therefore we obtain,
Now multiplying and dividing by 9 we obtain,
![]() terms
terms ![]()
![]()
![]() to
to ![]() terms
terms ![]()
Therefore the terms are in G.P
Where, ![]()
Using the formula,
The sum of GP for ![]() terms
terms ![]()
![Rendered by QuickLaTeX.com \begin{array}{l} 7 / 9\left[10\left(10^{n}-1\right) /(10-1)\right]-n \\ 7 / 9\left[10 / 9\left(10^{n}-1\right)-n\right] \\ 7 / 81\left[10\left(10^{n}-1\right)-n\right] \\ 7 / 81\left(10^{n+1}-9 n-10\right) \end{array}](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-531a3e690a5fdd2ee3e501d8d98d1fd4_l3.png)
