Note: The sum of the series is already provided in the question. The solution
to find x is given below.
Let there be n terms in the series.
x = 1 + (n – 1)3
= 3n – 2
Let S be the sum of the series

⇒ n[1 + 3n – 2] = 1430
⇒ n + 3n2 – 2n = 1430
⇒ 3n2 – n – 1430 = 0
Applying Sri Dhar Acharya formula, we get

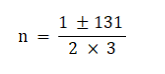
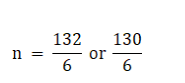
⇒ n = 22 as n cannot be a fraction
Therefore x = 3 × 22 – 2 = 64
The value of x is 64