Solution:
It is given that ![]() are in the form of AP in which
are in the form of AP in which ![]() for all i.
for all i.
To prove that:
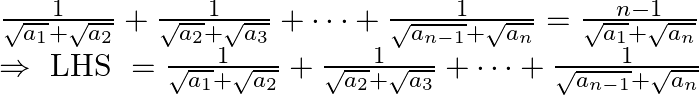
Multiply first term by 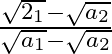 , the second term by
, the second term by 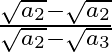 and so on i.e., rationalizing each term
and so on i.e., rationalizing each term
![]() Left Hand Side
Left Hand Side 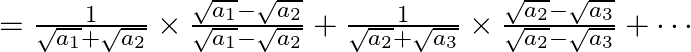
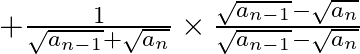
By using ![]()
![]() Left Hand Side
Left Hand Side ![]()
Since ![]() are in AP let us assume ‘d’ as its common difference
are in AP let us assume ‘d’ as its common difference
![]()
As a result multiplying by ![]()
![]()
On putting these values in the Left Hand Side, we get
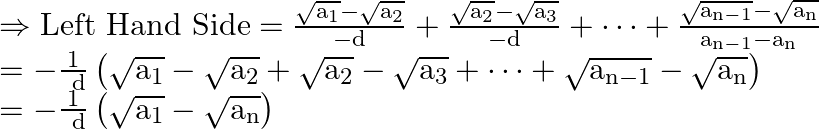
In the above equation multiply and divide by
![]()
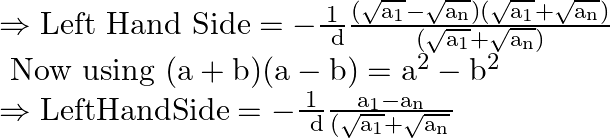
The ![]() term of the AP is
term of the AP is ![]()
In which the ![]() is last
is last ![]() term and
term and
![]() is first term
is first term
As a result ![]()
![]()
Now, substitute ![]() in Left Hand Side
in Left Hand Side
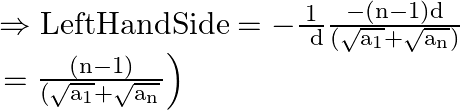
![]()
As a result hence proved.
