Solution:
As per the question,
![]()
We need to prove:
![]()
Proof:
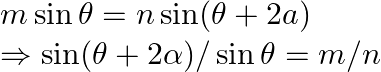
Now, apply the componendo-dividendo rule, so we have,
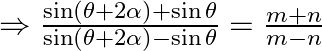
Using the transformation formula of T-ratios,
It is known that,
![]()
And,
![]()
By using the formula, we have,
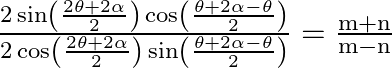
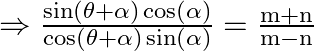
![]()
![]()
So, ![]() cot
cot ![]()
As a result, hence proved.
Solution:
As per the question,
![]()
We need to prove:
![]()
Proof:
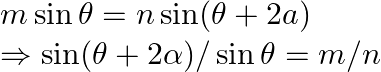
Now, apply the componendo-dividendo rule, so we have,
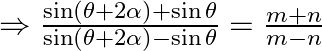
Using the transformation formula of T-ratios,
It is known that,
![]()
And,
![]()
By using the formula, we have,
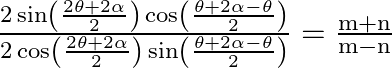
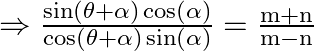
![]()
![]()
So, ![]() cot
cot ![]()
As a result, hence proved.