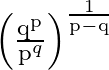Solution:
The ![]() term of Geometric Progression is given by
term of Geometric Progression is given by ![]() in which the first term is
in which the first term is ![]() and the common difference is
and the common difference is ![]()
![]() term is given as
term is given as ![]()
![]()
Above equation can also be re-written as
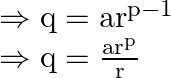
When we rearrange the above equation we obtain
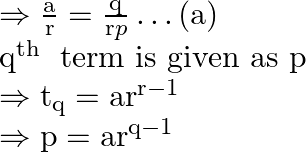
Above equation can also be re-written as
![]()
When we rearrange the above equation we obtain
![]()
From eq.(a) and eq.(b) we have
![]()
When we rearrange we obtain
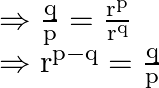
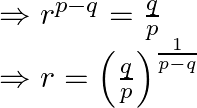
![]() term is given by
term is given by
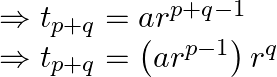
But ![]() and the
and the ![]() term is
term is ![]()
![]()
But
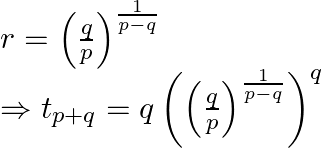
By using the laws of exponents we obtain
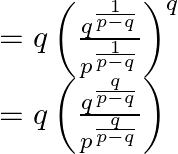
On rearranging
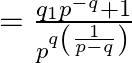
Now take LCM and simplify it
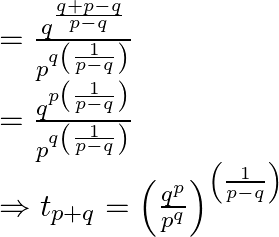
As a result hence proved.