Solution:
An AP’s sum of n terms is given by
![]()
Where the first term is ‘a’ and the common difference is ‘d’.
It is given that ![]() and
and ![]()
![]()
It is known that ![]()
![]()
Now rearrange
![]()
![]()
Again we have ![]()
![]()
When we rearrange we obtain
![]()
Subtract eq.(i) from eq.(ii) i.e. eq.(ii) – eq.(i)
![]()
Subtract eq.(i) from eq.(ii) i.e. eq.(ii) – eq.(i)
![]()
When we simplify we obtain
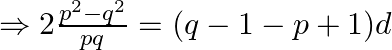
Using the ![]() formula we obtain
formula we obtain
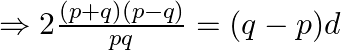
Compute and simplify now,
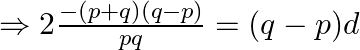
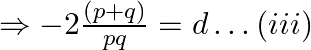
We need to show that ![]()
![]()
Above eq. can also be re-written as
![]()
![]()
![]()
Now using the ![]()
![]()
![]()
From eq.(iii) substitute ‘d’ 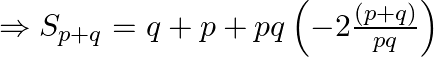
![]()
![]()
We now need to find the sum of ![]() terms that is
terms that is ![]()
![]()
![]()
The above eq. can also be re-written as
![]()
![]()
The above eq. can also be re-written as
![]()
![]()
Now using ![]() and
and ![]()
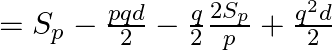
On substituting the value of ![]() we obtain
we obtain
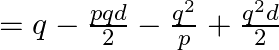
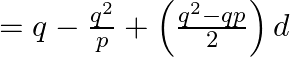
From eq.(iii) substitute ‘d’
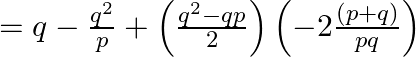
Simplify and compute now
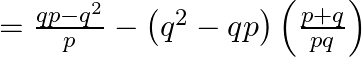
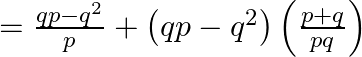
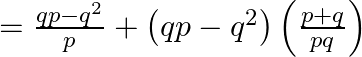
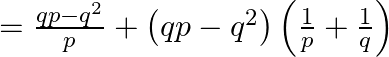
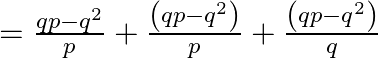
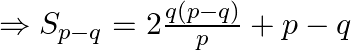
As a result the sum of ![]() terms is
terms is