Login/Sign Up
Home » If are in A.P., whose common difference is d, show that
If \theta_{1}, \theta_{2}, \theta_{3}, \ldots, \theta_{n} are in A.P., whose common difference is d, show that \operatorname{Sec} \theta_{1} \sec \theta_{2}+\sec \theta_{2} \sec \theta_{3}+\ldots+\sec \theta_{n-1} \sec \theta_{n}=\frac{\tan \theta_{\mathrm{n}}-\tan \theta_{1}}{\operatorname{sind}}
CBSE | Class 11 | Maths | NCERT Exemplar | Sequences and Series
If \theta_{1}, \theta_{2}, \theta_{3}, \ldots, \theta_{n} are in A.P., whose common difference is d, show that \operatorname{Sec} \theta_{1} \sec \theta_{2}+\sec \theta_{2} \sec \theta_{3}+\ldots+\sec \theta_{n-1} \sec \theta_{n}=\frac{\tan \theta_{\mathrm{n}}-\tan \theta_{1}}{\operatorname{sind}}

Solution:

It is given that \theta_{1}, \theta_{2}, \theta_{3}, \ldots, \theta_{n} are in the form of A.P., and d is the common difference,

We now need to prove that

\operatorname{Sec} \theta_{1} \sec \theta_{2}+\sec \theta_{2} \sec \theta_{3}+\ldots+\sec \theta_{n-1} \sec \theta_{n}=\frac{\tan \theta_{\mathrm{n}}-\tan \theta_{1}}{\operatorname{sind}}

When we cross multiply we obtain

\Rightarrow \sin d\left(\sec \theta_{1} \sec \theta_{2}+\sec \theta_{2} \sec \theta_{3}+\ldots+\sec \theta_{n-1} \sec \theta_{n}\right)=\tan \theta_{n}-\tan \theta_{1}

It is known \sec x=1 / \cos x so utilizing this formula we obtain

\Rightarrow \frac{\text { sind }}{\cos \theta_{1} \cos \theta_{2}}+\frac{\operatorname{sind}}{\cos \theta_{2} \cos \theta_{3}}+\cdots+\frac{\text { sind }}{\cos \theta_{n-1} \cos \theta_{n}}=\tan \theta_{n}-\tan \theta_{1}

Now consider the Left Hand Side

\Rightarrow Left Hand Side =\frac{\text { sind }}{\cos \theta_{1} \cos \theta_{2}}+\frac{\operatorname{sind}}{\cos \theta_{2} \cos \theta_{3}}+\cdots+\frac{\text { sind }}{\cos \theta_{n-1} \cos \theta_{n}}

We now need to find the value of \mathrm{d} in terms of \theta in order to simplify further.

As \theta_{1}, \theta_{2}, \theta_{3}, \ldots, \theta_{n} are in AP having common difference as \mathrm{d}

Therefore

\theta_{2}-\theta_{1}=\mathrm{d}, \theta_{3}-\theta_{2}=\mathrm{d}, \ldots, \theta_{\mathrm{n}}-\theta_{\mathrm{n}-1}=\mathrm{d}

On both sides taking sin

\operatorname{Sin}\left(\theta_{2}-\theta_{1}\right)=\sin d, \sin \left(\theta_{3}-\theta_{2}\right)=\sin d, \ldots, \sin \left(\theta_{n}-\theta_{n-1}\right)=\sin d

Now substitute the value of sin d for each term in Left Hand Side

\Rightarrow Left Hand Side =\frac{\sin \left(\theta_{2}-\theta_{1}\right)}{\cos \theta_{1} \cos \theta_{2}}+\frac{\sin \left(\theta_{3}-\theta_{2}\right)}{\cos \theta_{2} \cos \theta_{3}}+\cdots+\frac{\sin \left(\theta_{\mathrm{n}}-\theta_{\mathrm{n}-1}\right)}{\cos \theta_{\mathrm{n}-1} \cos \theta_{\mathrm{n}}}

It is known that \sin (\mathrm{a}-\mathrm{b})=\sin \mathrm{a} \cos \mathrm{b}-\cos \mathrm{a} \sin \mathrm{b}

Utilize this formula to obtain

\Rightarrow Left Hand Side

\begin{array}{r}=\frac{\sin \theta_{2} \cos \theta_{1}-\cos \theta_{2} \sin \theta_{1}}{\cos \theta_{1} \cos \theta_{2}}+\frac{\sin \theta_{3} \cos \theta_{2}-\cos \theta_{3} \sin \theta_{2}}{\cos \theta_{2} \cos \theta_{3}}+\cdots \\ +\frac{\sin \theta_{n} \cos \theta_{\mathrm{n}-1}-\cos \theta_{\mathrm{n}} \sin \theta_{\mathrm{n}-1}}{\cos \theta_{\mathrm{n}-1} \cos \theta_{\mathrm{n}}} \end{array}

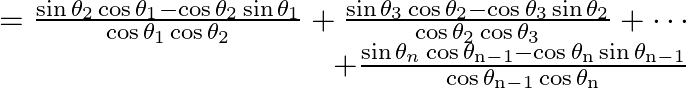
On simplying

\begin{array}{c} =\frac{\sin \theta_{2} \cos \theta_{1}}{\cos \theta_{1} \cos \theta_{2}}-\frac{\cos \theta_{2} \sin \theta_{1}}{\cos \theta_{1} \cos \theta_{2}}+\frac{\sin \theta_{3} \cos \theta_{2}}{\cos \theta_{2} \cos \theta_{3}}-\frac{\cos \theta_{3} \sin \theta_{2}}{\cos \theta_{2} \cos \theta_{3}}+\cdots +\frac{\sin \theta_{n} \cos \theta_{n-1}}{\cos \theta_{n-1} \cos \theta_{n}} \\-\frac{\cos \theta_{n} \sin \theta_{n-1}}{\cos \theta_{n-1} \cos \theta_{n}}{} \end{array}

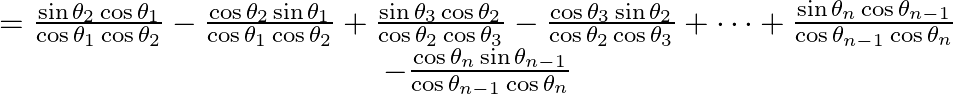
Known that \sin x / \cos x=\tan x

\begin{array}{l} =\tan \theta_{2}-\tan \theta_{1}+\tan \theta_{3}-\tan \theta_{2}+\ldots+\tan \theta_{n}-\tan \theta_{n-1} \\ =-\tan \theta_{1}+\tan \theta_{n} \\ =\tan \theta_{n}-\tan \theta_{1} \\ \end{array}

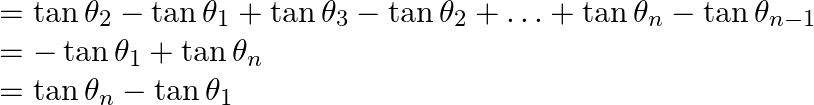
\Rightarrow Left Hand Side = Right Hand Side

As a result, hence proved.

i

More Material