Solution: Assume there be a system of n simultaneous linear equations and with ‘n’ unknown given by
![]()
![]()
![]()
 Let
Let ![]() be the determinant obtained from D after replacing the
be the determinant obtained from D after replacing the ![]() column by
column by
![]() Then,
Then,
![]() provided that
provided that ![]()
![]()
![]()
So by comparing with the theorem, let’s find ![]()
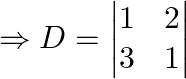
Solving for the determinant, expanding along 1st row
![]()
![]()
![]()
Again,
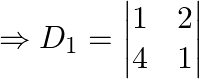
Solving for the determinant, expanding along 1st row
![]()
![]()
![]()
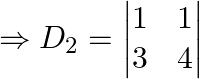
Solving for the determinant, expanding along 1st row
⇒ ![]()
⇒ ![]()
⇒ ![]()
Therefore, by Cramer’s Rule, we will get
![]()
![]()
![]()
And
![]()
![]()
![]()
