Answer:
The intersection of the lines: 3x + 2y = 11 and 2x + 3y = 4 Is (5, – 2)
The general form of the equation of a circle is (x – h)2 + (y – k)2 = r2
(h, k) is the centre of the circle. r is the radius of the circle.
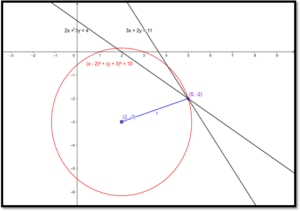
(h, k) = (2, – 3)
For determining the equation of the circle we need to determine the radius of the circle.
The circle passes through (5, – 2), that pair of values for x and y must satisfy the equation.
(5 – 2)2 + ( – 2 – ( – 3))2 = r2
32 + 12 = r2
r2 = 9 + 1
∴ r2 = 10
The equation of circle is,
(x – 2)2 + (y – ( – 3))2 = 10
(x – 2)2 + (y + 3)2 = 10
