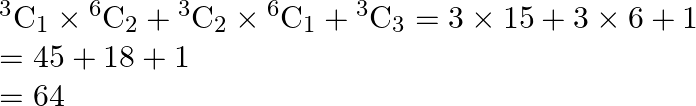Login/Sign Up
Home » A box contains two white, three black and four red balls. In how many ways can three balls be drawn from the box, if at least one black ball is to be included in the draw.[Hint: Required number of ways .]
A box contains two white, three black and four red balls. In how many ways can three balls be drawn from the box, if at least one black ball is to be included in the draw.[Hint: Required number of ways ={ }^{3} \mathbf{C}_{1} \times{ }^{6} \mathrm{C}_{2}+{ }^{3} \mathrm{C}_{2} \times^{6} \mathrm{C}_{1}+{ }^{3} \mathrm{C}_{3}.]
CBSE | Class 11 | Maths | NCERT Exemplar | Permutations and Combinations
A box contains two white, three black and four red balls. In how many ways can three balls be drawn from the box, if at least one black ball is to be included in the draw.[Hint: Required number of ways ={ }^{3} \mathbf{C}_{1} \times{ }^{6} \mathrm{C}_{2}+{ }^{3} \mathrm{C}_{2} \times^{6} \mathrm{C}_{1}+{ }^{3} \mathrm{C}_{3}.]

Solution:

It is known that,

=\frac{{ }^{n} C_{r}}{r !(n-r) !}

Now, drawing 1 black and 2 other ball ={ }^{3} \mathrm{C}_{1} \times{ }^{6} \mathrm{C}_{2}

Now, drawing 2 black and 1 other ball ={ }^{3} \mathrm{C}_{2} \times{ }^{6} \mathrm{C}_{1}

Now, drawing 3 black balls ={ }^{3} \mathrm{C}_{3}

The no. of ways in which at least one black ball can be drawn =

=(1 black and 2 other ) \operatorname{or}(2 black and 1 other ) or ( 3 black)

\begin{array}{l} { }^{3} \mathrm{C}_{1} \times{ }^{6} \mathrm{C}_{2}+{ }^{3} \mathrm{C}_{2} \times{ }^{6} \mathrm{C}_{1}+{ }^{3} \mathrm{C}_{3}=3 \times 15+3 \times 6+1 \\ =45+18+1 \\ =64 \end{array}

i

More Material