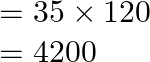Solution:
It is known that
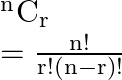
As per the question,
There are a total of 10 person named ![]()
The no. of ways in which ![]() can be arranged
can be arranged ![]()
The no. of ways in which the others can be arranged,
![]()
As a result, the required number of arrangement ![]()
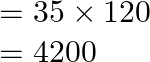
Solution:
It is known that
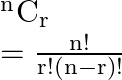
As per the question,
There are a total of 10 person named ![]()
The no. of ways in which ![]() can be arranged
can be arranged ![]()
The no. of ways in which the others can be arranged,
![]()
As a result, the required number of arrangement ![]()