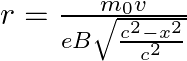(a) A monoenergetic electron beam with an electron speed of $5.20 \times 10^{6} \mathrm{~m} \mathrm{~s}^{-1}$ is subject to a magnetic field of $1.30 \times 10^{-4} \mathrm{~T}$ normal to the beam velocity. What is the radius of the circle traced by the beam, given e/m for electron equals $1.76 \times 10^{11} \mathrm{C} \mathrm{kg}^{-1}$.(b) Is the formula you employ in (a) valid for calculating the radius of the path of a $20 \mathrm{MeV}$ electron beam? If not, in what way is it modified?

Home » (a) A monoenergetic electron beam with an electron speed of is subject to a magnetic field of normal to the beam velocity. What is the radius of the circle traced by the beam, given e/m for electron equals .(b) Is the formula you employ in (a) valid for calculating the radius of the path of a electron beam? If not, in what way is it modified?

(a) A monoenergetic electron beam with an electron speed of $5.20 \times 10^{6} \mathrm{~m} \mathrm{~s}^{-1}$ is subject to a magnetic field of $1.30 \times 10^{-4} \mathrm{~T}$ normal to the beam velocity. What is the radius of the circle traced by the beam, given e/m for electron equals $1.76 \times 10^{11} \mathrm{C} \mathrm{kg}^{-1}$ .

(b) Is the formula you employ in (a) valid for calculating the radius of the path of a $20 \mathrm{MeV}$ electron beam? If not, in what way is it modified?

CBSE | Class 12 | Dual Nature of Radiation and Matter | NCERT | Physics

(a) A monoenergetic electron beam with an electron speed of $5.20 \times 10^{6} \mathrm{~m} \mathrm{~s}^{-1}$ is subject to a magnetic field of $1.30 \times 10^{-4} \mathrm{~T}$ normal to the beam velocity. What is the radius of the circle traced by the beam, given e/m for electron equals $1.76 \times 10^{11} \mathrm{C} \mathrm{kg}^{-1}$ .

(b) Is the formula you employ in (a) valid for calculating the radius of the path of a $20 \mathrm{MeV}$ electron beam? If not, in what way is it modified?

Magnetic field experienced by the electron, $B=1.30 \times 10^{-4} \mathrm{~T}$

Specific charge, e/m is given by $=1.76 \times 10^{11} \mathrm{Ckg}^{-1}$

Here,

$e=$ charge on the electron $=1.6 \times 10^{-19} \mathrm{C}$

$m=$ mass of the electron $=9.1 \times 10^{-31} \mathrm{~kg}^{-1}$

The force exerted on the electron can be written as:

$F=e|\vec{v} \times \vec{B}|$

$=\operatorname{evBsin} \theta$

The angle between the magnetic field and the beam’s velocity is $\theta$ . The magnetic field is perpendicular to the beam’s direction.

$\theta=90^{\circ}$

$F=e v B$

As the normal magnetic field provides the centripetal force, so we can write

evB $=\mathrm{mv}^{2} / \mathrm{r}$

$r=m v / e B=v /(e / m) B$

$=\left(5.20 \times 10^{6}\right) /\left(1.76 \times 10^{11}\right) \times\left(1.30 \times 10^{-4}\right)=0.227 \mathrm{~m}=22.7 \mathrm{~cm}$

Therefore, $22.7 \mathrm{~cm}$ is the radius of the circular path.

(b) Energy of the electron beam is given as $E=20 \mathrm{Mev}=20 \times 10^{6} \times 1.6 \times 10^{-19} \mathrm{~J}$

The energy of the electron beam is given by the expression,
$E=(1 / 2) \mathrm{mv}^{2}$

$\Rightarrow v=\sqrt{\frac{2 E}{m}}$

$v=\sqrt{\frac{2 \times 20 \times 10^{6} \times 1.6 \times 10^{-19}}{9.1 \times 10^{-31}}}=2.652 \times 10^{9} \mathrm{~m} / \mathrm{s}$

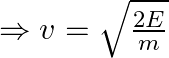
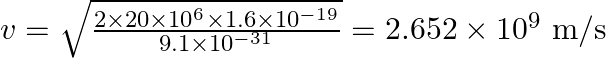
We can see that the result is greater than the speed of light. So, it is wrong. The expression $(1 / 2) \mathrm{mv}^{2}$ for energy should be used in the non -relativistic limit. i.e., $v<<c$ .