Login/Sign Up
Home » A rocket is fired vertically with a speed of from the earth’s surface. How far from the earth does the rocket go before returning to the earth? Mass of the earth ; mean radius of the earth
A rocket is fired vertically with a speed of 5 \mathrm{~km} \mathrm{~s}^{-1} from the earth’s surface. How far from the earth does the rocket go before returning to the earth? Mass of the earth =6.0 \times 10^{24} \mathrm{~kg}; mean radius of the earth =6.4 \times 10^{6} \mathrm{~m} ; \mathbf{G}=6.67 \times 10^{-11} \mathrm{~N} \mathrm{~m}^{2} \mathrm{~kg}^{-2} .
CBSE | Class 11 | Gravitation | NCERT | Physics
A rocket is fired vertically with a speed of 5 \mathrm{~km} \mathrm{~s}^{-1} from the earth’s surface. How far from the earth does the rocket go before returning to the earth? Mass of the earth =6.0 \times 10^{24} \mathrm{~kg}; mean radius of the earth =6.4 \times 10^{6} \mathrm{~m} ; \mathbf{G}=6.67 \times 10^{-11} \mathrm{~N} \mathrm{~m}^{2} \mathrm{~kg}^{-2} .

Velocity of the missile is given as v=5 \times 10^{3} \mathrm{~m} / \mathrm{s}

Mass of the Earth is known as M_{E}=6 \times 10^{24} \mathrm{~kg}

Radius of the Earth is given as R_{E}=6.4 \times 10^{6} \mathrm{~m}

Let, the mass of the missile be ‘ m ‘ and the height reached by the missile be ‘ h ‘.

At the surface of the Earth:

The total energy of the rocket at the surface of the Earth will be equal to the sum of Kinetic energy and Potential energy.

\mathrm{T}_{\mathrm{E} 1}=\frac{1}{2} m v^{2}+\frac{-G M_{E} m}{R_{E}}

At the highest point ‘ h ‘:

Kinetic Energy =0 \quad

And, Potential energy =\frac{-G M_{E} m}{R_{E}+h}

Therefore, total energy of the missile at highest point ‘ h ‘ according to the relation above:

\mathrm{T}_{\mathrm{E} 2}=0+\frac{-G M_{E} \mathrm{~m}}{R_{E}+h} \Rightarrow \mathrm{T}_{\mathrm{E} 2}=\frac{-G M_{E} \mathrm{~m}}{R_{E}+h}

According to the law of conservation of energy, we can say:

Total energy of the rocket at the Earth’s surface T_{E 1}= Total energy at height ‘ h ‘ T_{E 2} :

\frac{1}{2}m{{v}^{2}}+\frac{-G{{M}_{e}}m}{{{R}_{E}}}=\frac{-G{{M}_{e}}m}{{{R}_{E}}+h}

\frac{1}{2}{{v}^{2}}+\frac{-G{{M}_{E}}}{{{R}_{E}}}=\frac{-G{{M}_{E}}m}{{{R}_{E}}+h}

{{v}^{2}}=2G{{M}_{E}}\times [\frac{1}{{{R}_{E}}}-\frac{1}{({{R}_{E}}+h)}]=2G{{M}_{E}}[\frac{h}{({{R}_{E}}+h){{R}_{E}}}]

{{v}^{2}}=\frac{G{{M}_{E}}h}{{{R}^{2}}_{E}+{{R}_{h}}}

Where,

g=\frac{G M}{R_{E}^{2}}=9.8 \mathrm{~ms}^{-2}

V^{2}=2 g R_{E}^{2} h / R_{E}^{2}+R_{E} h

\Rightarrow v^{2}=\frac{2 g R_{E} h}{R_{E}+h}

Therefore, \mathrm{v}^{2}\left(\mathrm{R}_{\mathrm{E}}+\mathrm{h}\right)=2 \mathrm{gR}_{\mathrm{E}} \mathrm{h}

\Rightarrow v^{2} R_{E}=h\left(2 g R_{E}-v^{2}\right)

\Rightarrow h=\frac{R_{E} v^{2}}{2 g R_{E}-v^{2}}=\frac{\left(6.4 \times 10^{6}\right) \times\left(5 \times 10^{3}\right)^{2}}{2 \times 9.8 \times 6.4 \times 10^{6}-\left(5 \times 10^{3}\right)^{2}}

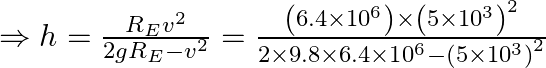
Now, the distance from the center of the earth is 8.0 \times 10^{6} \mathrm{~m}

i

More Material