Find the area of the circle $4x^{2}+4y^{2}=9$ which is interior to the parabola $x^{2}=4y$.

Home » Find the area of the circle which is interior to the parabola .

Find the area of the circle $4x^{2}+4y^{2}=9$ which is interior to the parabola $x^{2}=4y$ .

Find the area of the circle $4x^{2}+4y^{2}=9$ which is interior to the parabola $x^{2}=4y$ .

Solution:

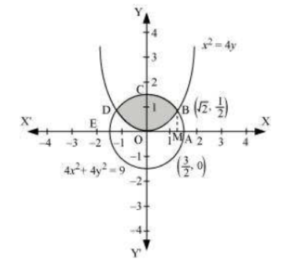
Required area is represented by the shaded area OBCDO

On solving the given equation of circle, $4 x^{2}+4 y^{2}=9$ , and parabola, $x^{2}=4 y$ , we get $\mathrm{B}\left(\sqrt{2}, \frac{1}{2}\right)$ and $\mathrm{D}\left(-\sqrt{2}, \frac{1}{2}\right)$
It is observed that the area required is symmetrical about $y$ -axis.
$\therefore$ Area $\mathrm{OBCDO}=2 \times$ Area $\mathrm{OBCO}$
We draw BM perpendicular to OA.
So, the coordinates of $\mathrm{M}$ are $^{(\sqrt{2}, 0)} .$
As a result, Area of OBCO $=$ Area of OMBCO – Area of OMBO
$\begin{array}{l} =\int_{0}^{\sqrt{2}} \sqrt{\frac{\left(9-4 x^{2}\right)}{4}} d x-\int_{0}^{\sqrt{2}} \sqrt{\frac{x^{2}}{4}} d x \\ =\frac{1}{2} \int_{0}^{\sqrt{2}} \sqrt{9-4 x^{2}} d x-\frac{1}{4} \int_{0}^{\sqrt{2}} x^{2} d x \\ =\frac{1}{4}\left[x \sqrt{9-4 x^{2}}+\frac{9}{2} \sin ^{-1} \frac{2 x}{3}\right]_{0}^{\sqrt{2}}-\frac{1}{4}\left[\frac{x^{3}}{3}\right]_{0}^{\sqrt{2}} \\ =\frac{1}{4}\left[\sqrt{2} \sqrt{9-8}+\frac{9}{2} \sin ^{-1} \frac{2 \sqrt{2}}{3}\right]-\frac{1}{12}(\sqrt{2})^{3} \\ =\frac{\sqrt{2}}{4}+\frac{9}{8} \sin ^{-1} \frac{2 \sqrt{2}}{3}-\frac{\sqrt{2}}{6} \\ =\frac{\sqrt{2}}{12}+\frac{9}{8} \sin ^{-1} \frac{2 \sqrt{2}}{3} \\ =\frac{1}{2}\left(\frac{\sqrt{2}}{6}+\frac{9}{4} \sin ^{-1} \frac{2 \sqrt{2}}{3}\right) \end{array}$
As a result, the required area OBCDO is
$\left(2 \times \frac{1}{2}\left[\frac{\sqrt{2}}{6}+\frac{9}{4} \sin ^{-1} \frac{2 \sqrt{2}}{3}\right]\right)=\left[\frac{\sqrt{2}}{6}+\frac{9}{4} \sin ^{-1} \frac{2 \sqrt{2}}{3}\right]_{\text {units }}$