Let ![]() and
and ![]() be the given points.
be the given points.
=> ![]()
![]()
![]() sq. units
sq. units
=> the area of the triangle ![]() is 4 sq. units
is 4 sq. units
Let ![]() and
and ![]() be the midpoints of
be the midpoints of ![]() and
and ![]() respectively Then
respectively Then
![]()
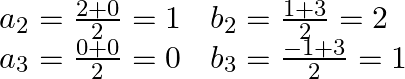
=> the coordinates of ![]() and Fare
and Fare ![]() and
and
![]() Now
Now
Area ![]()
![]()
![]() sq. unit
sq. unit
=> the area of the triangle ![]() is 1 sq. unit.
is 1 sq. unit.
Therefore, ![]()
