Login/Sign Up
Home » Find the derivative of the following functions (it is to be understood that  and  are fixed non-zero constants and  and  are integers): .
Find the derivative of the following functions (it is to be understood that a,b,c,d,p,q,r and s are fixed non-zero constants and m and n are integers): {\sin ^n}x.
CBSE | Class 11 | Limits and Derivatives | Maths | Miscellaneous Exercise | NCERT
Find the derivative of the following functions (it is to be understood that a,b,c,d,p,q,r and s are fixed non-zero constants and m and n are integers): {\sin ^n}x.

Assume, y = {\sin ^n}x

When n = 1, then

y = \sin x

Differentiating with respect to x we get,

\frac{{dy}}{{dx}} = \cos x

This implies, \frac{d}{{dx}}\sin x = \cos x.

Now when n = 2, then

y = {\sin ^2}x

\frac{{dy}}{{dx}} = \frac{d}{{dx}}(\sin x\sin x)

Applying Leibnitz product rule to get,

\frac{{dy}}{{dx}} = {(\sin x)^\prime }\sin x + \sin x{(\sin x)^\prime }

\frac{{dy}}{{dx}} = \cos x\sin x + \sin x\cos x

\frac{{dy}}{{dx}} = 2\sin x\cos x                              …… (1)

Also, when n = 3, then

y = {\sin ^3}x

Applying Leibnitz product rule to get,

\frac{{dy}}{{dx}} = {(\sin x)^\prime }{\sin ^2}x + \sin x{\left( {{{\sin }^2}x} \right)^\prime }

So, substituting equation (1) to get,

\frac{{dy}}{{dx}} = \cos x{\sin ^2}x + \sin x(2\sin x\cos x)

\frac{{dy}}{{dx}} = \cos x{\sin ^2}x + 2{\sin ^2}x\cos x

\frac{{dy}}{{dx}} = 3{\sin ^2}x\cos x

From the above we can state that,

\frac{d}{{dx}}\left( {{{\sin }^n}x} \right) = n{\sin ^{(n - 1)}}x\cos x

For n = k, let this assertion be true,

\frac{d}{{dx}}\left( {{{\sin }^k}x} \right) = k{\sin ^{(k - 1)}}x\cos x                 …… (2)

Let us consider,

\frac{d}{{dx}}\left( {{{\sin }^{k + 1}}x} \right) = \frac{d}{{dx}}\left( {\sin x{{\sin }^k}x} \right)

Applying Leibnitz product rule to get,

\frac{{dy}}{{dx}} = {(\sin x)^\prime }{\sin ^k}x + \sin x{\left( {{{\sin }^k}x} \right)^\prime }

So, substituting equation (2) to get,

\frac{{dy}}{{dx}} = \cos x{\sin ^k}x + \sin x\left( {k{{\sin }^{(k - 1)}}x\cos x} \right)

\frac{{dy}}{{dx}} = \cos x{\sin ^k}x + k{\sin ^k}x\cos x

\frac{{dy}}{{dx}} = (k + 1){\sin ^k}x\cos x

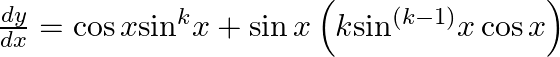
Hence, our assertion is true for n = k + 1.

Thus, by Mathematical Induction principle,

\frac{d}{{dx}}\left( {{{\sin }^n}x} \right) = n{\sin ^{(n - 1)}}x\cos x.

i

More Material