Solution:
![]()
To solve (1) we will use following formula
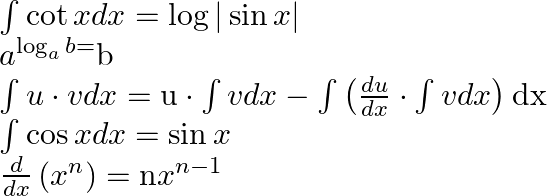
General solution for the differential equation in the form of ![]()
General solution is given by,
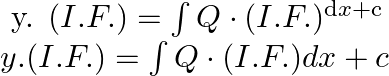
Where, integrating factor,
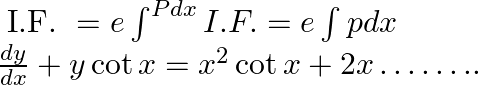
Equation (1) is of the form
![]()
Where, ![]() and
and ![]()
Therefore, integrating factor is
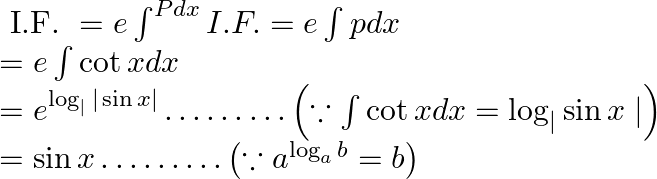
General solution is
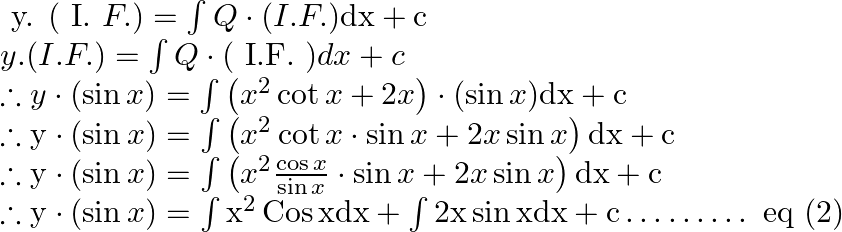
![]()
Let, ![]() and
and ![]()
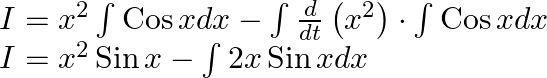
Substituting I in (2),
![]()
Dividing above equation by ![]() ,
,
![]()
Therefore, general solution is
![]()
