Solution:
(i) The criteria of existence of inverse matrix is the determinant of a given matrix should not be equal to zero.
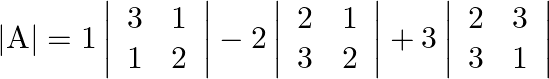
![]()
![]()
![]()
Thus, ![]() exists
exists
Cofactors of ![]() are
are
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
It is known that adi ![Rendered by QuickLaTeX.com A=\left[\begin{array}{lll}\mathrm{C}_{11} & \mathrm{C}_{12} & \mathrm{C}_{13} \\ \mathrm{C}_{21} & \mathrm{C}_{22} & \mathrm{C}_{23} \\ \mathrm{C}_{31} & \mathrm{C}_{32} & \mathrm{C}_{33}\end{array}\right]^{\mathrm{T}}](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-9676417b83389d11f27afac1beba4e67_l3.png)
![Rendered by QuickLaTeX.com =\left[\begin{array}{ccc}5 & -1 & -7 \\ -1 & -7 & 5 \\ -7 & 5 & -1\end{array}\right]^{\mathrm{T}}](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-e0d2d125237e4b24adc50df98c07a205_l3.png)
Therefore, adj ![Rendered by QuickLaTeX.com A=\left[\begin{array}{ccc}5 & -1 & -7 \\ -1 & -7 & 5 \\ -7 & 5 & -1\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-f5d0f43f2b8ae38e0d62babddbb223b8_l3.png) Now,
Now, ![]() adj
adj ![]()
Therefore, ![Rendered by QuickLaTeX.com A^{-1}=\frac{1}{(-18)}\left[\begin{array}{ccc}5 & -1 & -7 \\ -1 & -7 & 5 \\ -7 & 5 & -1\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-3e531eef56bdd1dff682f64ea8c5edc6_l3.png)
Thus,
![Rendered by QuickLaTeX.com A^{-1}=\left[\begin{array}{ccc} \frac{-5}{18} & \frac{1}{18} & \frac{7}{18} \\ \frac{1}{18} & \frac{7}{18} & \frac{-5}{18} \\ \frac{7}{18} & \frac{-5}{18} & \frac{1}{18} \end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-83bb5153140ee1265cde9ef75a2e522c_l3.png)
(ii) The criteria of existence of inverse matrix is the determinant of a given matrix should not be equal to zero.
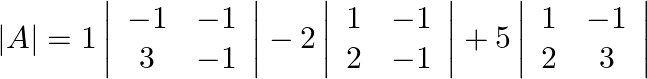
![]()
![]()
![]()
Thus, ![]() exists
exists
Cofactors of ![]() are
are
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \operatorname{adj} A=\left[\begin{array}{lll}C_{11} & C_{12} & C_{13} \\ C_{21} & C_{22} & C_{23} \\ C_{31} & C_{32} & C_{33}\end{array}\right]^{T}](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-9834afbe881cf199821120dac42e10e3_l3.png)
![Rendered by QuickLaTeX.com =\left[\begin{array}{ccc}4 & -1 & 5 \\ 17 & -11 & 1 \\ 3 & 6 & -3\end{array}\right]^{\mathrm{T}}](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-239182895210ac13b9db4b7ca96e3038_l3.png)
Therefore, adj ![Rendered by QuickLaTeX.com A=\left[\begin{array}{ccc}4 & 17 & 3 \\ -1 & -11 & 6 \\ 5 & 1 & -3\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-f58c5e30419c652ffb9d884e6ccd7cff_l3.png)
Now, ![]()
Therefore, ![Rendered by QuickLaTeX.com A^{-1}=\frac{1}{(27)}\left[\begin{array}{ccc}4 & 17 & 3 \\ -1 & -11 & 6 \\ 5 & 1 & -3\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-2d57d898d4dee0fae15b88bf1feb35b7_l3.png)
Thus, ![Rendered by QuickLaTeX.com \mathrm{A}^{-1}=\left[\begin{array}{ccc}\frac{4}{27} & \frac{17}{27} & \frac{3}{27} \\ \frac{-1}{27} & \frac{-11}{27} & \frac{6}{27} \\ \frac{5}{27} & \frac{1}{27} & \frac{-3}{27}\end{array}\right]=\left[\begin{array}{ccc}\frac{4}{27} & \frac{17}{27} & \frac{1}{9} \\ \frac{-1}{27} & \frac{-11}{27} & \frac{2}{9} \\ \frac{5}{27} & \frac{1}{27} & \frac{-1}{9}\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-02713d0bb58e65ff5ddc1d70d22e6309_l3.png)

![Rendered by QuickLaTeX.com \begin{aligned} &\text { (i) }\left[\begin{array}{lll} 1 & 2 & 3 \\ 2 & 3 & 1 \\ 3 & 1 & 2 \end{array}\right] \\ \end{aligned}](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-c6bff7bec98e31e88f08d3b006c1e4be_l3.png)
![Rendered by QuickLaTeX.com \begin{aligned} &\text { (ii) }\left[\begin{array}{ccc} 1 & 2 & 5 \\ 1 & -1 & -1 \\ 2 & 3 & -1 \end{array}\right] \\ \end{aligned}](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-a3b396c983282cb290a1787e6ea7e548_l3.png)