Solution:
Given matrix as 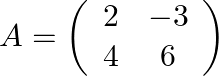 .
.
Now let’s calculate the determinant of the given matrix first.
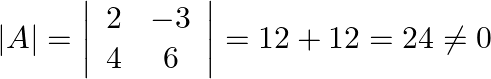
So the given matrix has inverse.
Find: the adjoint of the given matrix.
Step: 1 Find the minor matrix of ![]() .
.
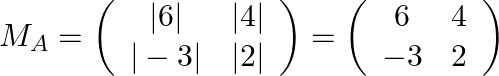
Step: 2 Find the co-factor matrix of ![]() .
.
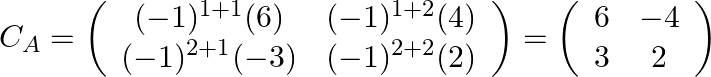
Step: 3 By transpose of ![]() we will have
we will have ![]() .
.
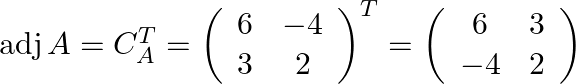
Finally the inverse of the matrix is
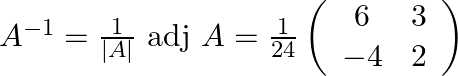

![Rendered by QuickLaTeX.com \left[\begin{array}{cc} 2 & -3 \\ 4 & 6 \end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-3b9bb3c6ff09639db2581255af80171d_l3.png)