Solution:
It is known to us that the polar form of a complex number ![]() iy is given by
iy is given by ![]()
In which,
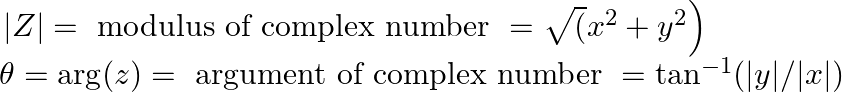
(i) ![]()
Given that ![]()
Let’s multiply and divide by ![]() , we get
, we get
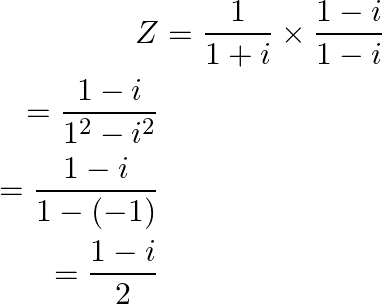
Therefore now,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
As ![]() complex number lies in
complex number lies in ![]() quadrant and the value of
quadrant and the value of ![]() is
is ![]() .
.
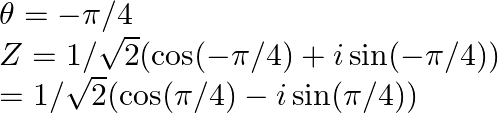
As a result, polar form of ![]() is
is ![]()
(ii) ![]()
Given that ![]()
Let’s multiply and divide by ![]() , we get
, we get
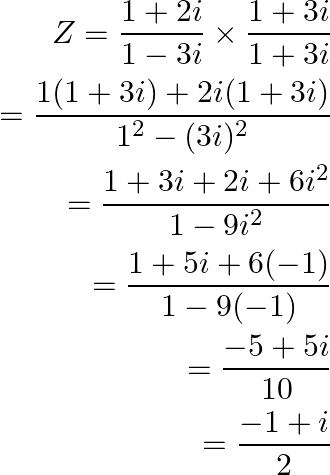
Therefore now,
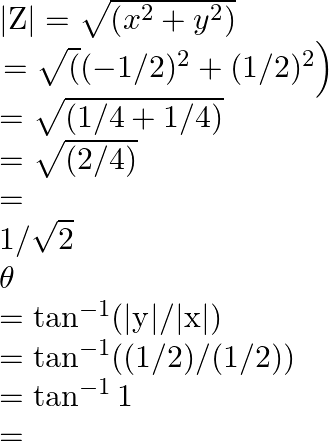
As ![]() complex number lies in
complex number lies in ![]() quadrant and the value of
quadrant and the value of ![]() is
is ![]()
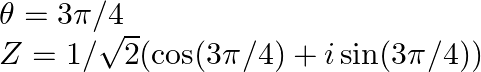
As a result, polar form of ![]() is
is ![]()
