Solution:
The system of equations:
![]()
![]()
And, ![]()
![]()
The equations are of the following form:
![]()
where, ![]() and
and ![]()
For an infinite number of solutions, we must have:
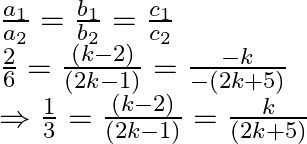
So now, we have the following three cases:
Case I:
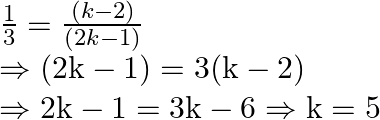
Case II:
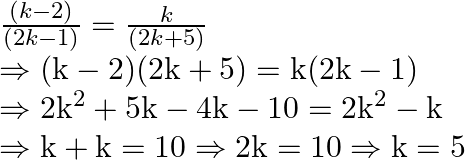
Case III:
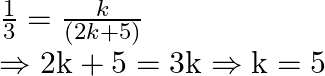
As a result, the given system of equations has an infinite number of solutions when ![]() is equal to 5
is equal to 5
