Solution:
We can write the given system of equations as
![]()
![]()
and ![]()
![]()
The given equations are of the following form:
![]()
where, ![]() and
and ![]()
For an infinite no. of solutions, we must have:
![Rendered by QuickLaTeX.com \begin{array}{l}\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}} \\ \frac{2}{(a+b+1)}=\frac{3}{(a+2 b+2)}=\frac{-7}{-[4(a+b)+1]} \\ \Rightarrow \frac{2}{(a+b+1)}=\frac{3}{(a+2 b+2)}=\frac{7}{[4(a+b)+1]} \\ \Rightarrow \frac{2}{(a+b+1)}=\frac{3}{(a+2 b+2)} \text { and } \frac{3}{(a+2 b+2)}=\frac{7}{[4(a+b)+1]} \\ \Rightarrow 2(a+2 b+2)=3(a+b+1) \text { and } 3[4(a+b)+1]=7(a+2 b+2) \\ \Rightarrow 2 a+4 b+4=3 a+3 b+3 \text { and } 3(4 a+4 b+1)=7 a+14 b+14 \\ \Rightarrow a-b-1=0 \text { and } 12 a+12 b+3=7 a+14 b+14 \\ \Rightarrow a-b=1 \text { and } 5 a-2 b=11 \\ a=(b+1) \quad \ldots \ldots \text { (iii) } \\ 5 a-2 b=11 \ldots \ldots \text { (iv) }\end{array}](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-83d464d50fe0c20499a4bd6cc40b5562_l3.png)
On substituting ![]() in equation(iv), we obtain:
in equation(iv), we obtain:
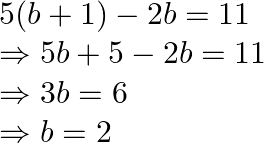
On substituting ![]() in equation(iii), we obtain:
in equation(iii), we obtain:
![]()
![]() and
and ![]()
