Login/Sign Up
Home » For what value of k, the system of equations Have (i) a unique solution, (ii) no solution? Also, show that there is no value of for which the given system of equation has infinitely namely solutions
For what value of k, the system of equations
x+2 y=3
5 x+k y+7=0 Have (i) a unique solution, (ii) no solution? Also, show that there is no value of \mathrm{k} for which the given system of equation has infinitely namely solutions
CBSE | Class 10 | Excercise 3D | Maths | Pair of Linear Equations in Two Variables | RS Aggarwal
For what value of k, the system of equations
x+2 y=3
5 x+k y+7=0 Have (i) a unique solution, (ii) no solution? Also, show that there is no value of \mathrm{k} for which the given system of equation has infinitely namely solutions

Solution:

The given system of equations:
\begin{array}{l} x+2 y=3 \\ \Rightarrow x+2 y-3=0\dots \dots(i) \end{array}
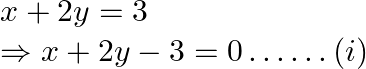
And, 5 x+k y+7=0\dots \dots(ii)
The equations are of the following form:
a_{1} x+b_{1} y+c_{1}=0, a_{2} x+b_{2} y+c_{2}=0
where, a_{1}=1, b_{1}=2, c_{1}=-3 and a_{2}=5, b_{2}=k, c_{2}=7

(i) For a unique solution, we must have:
\therefore \frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}} that is,\frac{1}{5} \neq \frac{2}{k} \Rightarrow \mathrm{k} \neq 10
Therefore for all the real values of \mathrm{k} other than 10, the given system of equations will have a unique solution.

(ii) In order that the given system of equations has no solution, we must have:
\begin{array}{l} \frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}} \\ \Rightarrow \frac{1}{5} \neq \frac{2}{k} \neq \frac{-3}{7} \\ \Rightarrow \frac{1}{5} \neq \frac{2}{k} \text { and } \frac{2}{k} \neq \frac{-3}{7} \\ \Rightarrow \mathrm{k}=10, \mathrm{k} \neq \frac{14}{-3} \end{array}
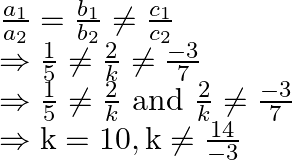
As a result, the required value of \mathrm{k} is 10
There is no value of k for which the given system of equations has an infinite number of solutions.

i

More Material