![\text { If } A=\left[\begin{array}{ll} 3 & 2 \\ 7 & 5 \end{array}\right] \text { and } B=\left[\begin{array}{ll} 6 & 7 \\ 8 & 9 \end{array}\right], \text { verify that }(A B)^{-1}=B^{-1} A^{-1} \text {. }](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-b2de5f0bf5c6ac098b6c2fce24f4632b_l3.png "Rendered by QuickLaTeX.com")
Solution:
Here,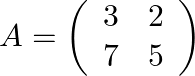 
and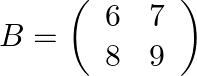 
Now find
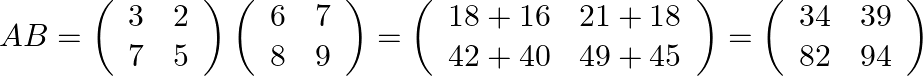
We now need to find the inverses of some matrices as below:
(i) Given matrix as .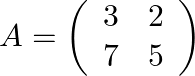
Let’s now calculate the determinant of the given matrix first.
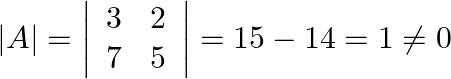
So, the given matrix has inverse.
Find: the adjoint of the given matrix.
Step: 1 Find the minor matrix of 
.
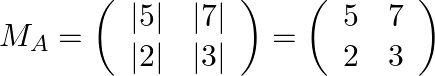
Step: 2 Find the co-factor matrix of .
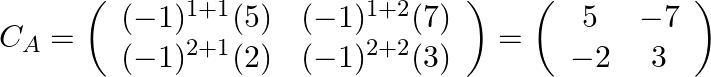
Step: 3 By transpose of 
we will have 
.
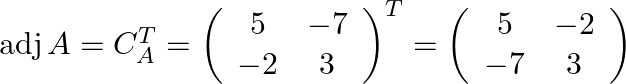
Finally the inverse of the matrix is
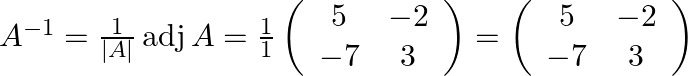
(ii) Given matrix as .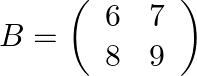
Let’s now calculate the determinant of the given matrix first.
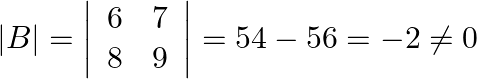
So, the given matrix has inverse.
Find: the adjoint of the given matrix.
Step: 1 Find the minor matrix of 
.
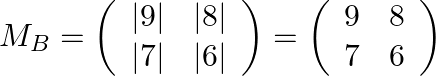
Step: 2 Find the co-factor matrix of .
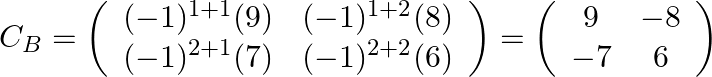
Step: 3 By transpose of 
we will have 
.
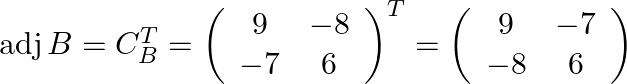
Finally the inverse of the matrix is
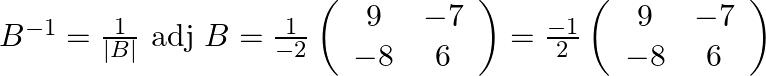
(iii) Given matrix as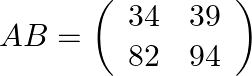 
.
Let’s now calculate the determinant of the given matrix first.
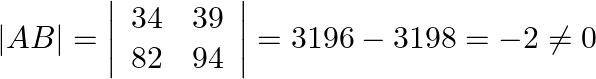
So, the given matrix has inverse.
Find: the adjoint of the given matrix.
Step: 1 Find the minor matrix of 
.
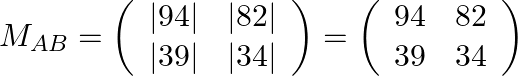
Step: 2 Find the co-factor matrix of .
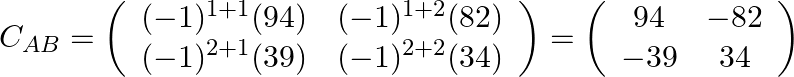
Step: 3 By transpose of 
we will have 
.
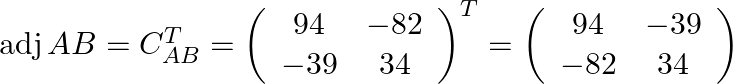
Finally the inverse of the matrix is
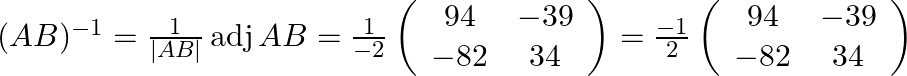
(iv) Now on finally multiplying the inverse of B with inverse of A we obtain
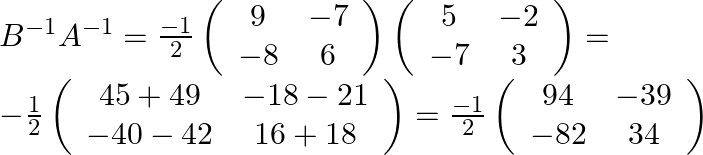
Hence, from the results of (iii) and (iv) we get 
.