Solution:
It is known to us that the angle between the lines with direction ratios ![]() and
and ![]() is given by
is given by
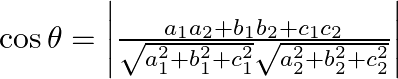
So, a line passing through ![]() and
and ![]() has direction ratios
has direction ratios ![]() The direction ratios of line joining the points
The direction ratios of line joining the points ![]() and
and ![]()
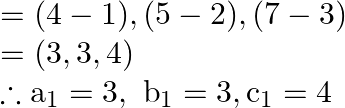
Direction ratios of line joining the points ![]() and
and ![]()
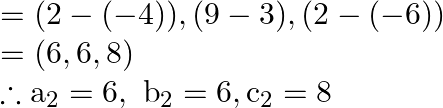
Let’s now substitute the values in the above equation we get,
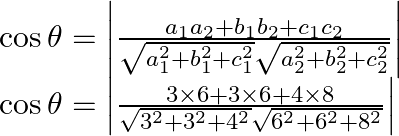
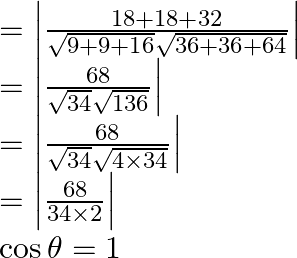
Therefore, ![]() since,
since, ![]() is 1
is 1![]()
As a result, Angle between the lines ![]() and
and ![]() is
is ![]() .
.
