If the points (1, 1, p) and (–3, 0, 1) be equidistant from the plane $\vec{r} \cdot(3 \hat{i}+4 \hat{j}-12 \hat{k})+13=0$, then find the value of $p$.

Home » If the points (1, 1, p) and (–3, 0, 1) be equidistant from the plane , then find the value of .

If the points (1, 1, p) and (–3, 0, 1) be equidistant from the plane $\vec{r} \cdot(3 \hat{i}+4 \hat{j}-12 \hat{k})+13=0$ , then find the value of $p$ .

If the points (1, 1, p) and (–3, 0, 1) be equidistant from the plane $\vec{r} \cdot(3 \hat{i}+4 \hat{j}-12 \hat{k})+13=0$ , then find the value of $p$ .

Solution:

It is known to us that the distance of a point with position vector $\vec{a}$ from the plane $\vec{r} \cdot \vec{n}=d$ is given as
$\left|\frac{\vec{a} \cdot \vec{n}-d}{|\vec{n}|}\right|$
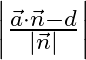
Now, the position vector of point $(1,1, p)$ is given as
$\overrightarrow{\mathrm{a}_{1}}=1 \hat{\mathrm{i}}+1 \hat{\mathrm{j}}+\mathrm{p} \hat{\mathrm{k}}$
And, the position vector of point $(-3,0,1)$ is given as
$\overrightarrow{\mathrm{a}_{2}}=-3 \hat{\mathrm{i}}+0 \hat{\mathrm{j}}+1 \hat{\mathrm{k}}$
It is given that the points $(1,1, \mathrm{p})$ and $(-3,0,1)$ are equidistant from the plane $\vec{r} \cdot(3 \hat{\mathrm{i}}+4 \hat{\mathrm{j}}-12 \hat{\mathrm{k}})+13=0$
Therefore,
$\left|\frac{(1 \hat{i}+1 \hat{j}+p \hat{k}) \cdot(3 \hat{i}+4 \hat{j}-12 \hat{k})+13}{\sqrt{3^{2}+4^{2}+(-12)^{2}}}\right| =\left|\frac{(-3 \hat{i}+0 \hat{j}+1 \hat{k}) \cdot(3 \hat{i}+4 \hat{j}-12 \hat{k})+13}{\sqrt{3^{2}+4^{2}+(-12)^{2}}}\right|$
$\begin{array}{l} \left|\frac{3+4-12 p+13}{\sqrt{9+16+144}}\right| =\left|\frac{-9+0-12+13}{\sqrt{9+16+144}}\right| \\ \left|\frac{20-12 p}{\sqrt{169}}\right| =\left|\frac{-8}{\sqrt{169}}\right| \\ |20-12 p|=8 \end{array}$
$\begin{array}{l} 20-12 p=\pm 8 \\ 20-12 p=8 \text { or, } 20-12 p=-8 \\ 12 p=12 \text { or }, 12 p=28 \\ p=1 \text { or, } p=7 / 3 \end{array}$
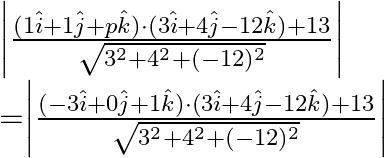
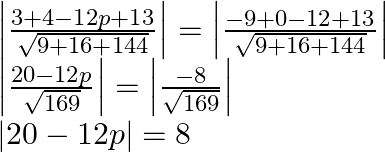
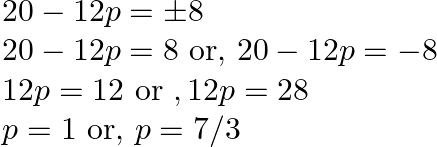
As a result, the possible values of $p$ are 1 and $7 / 3$ .