Solution:
![]() and
and ![]() (As given)
(As given)
Non-Reflexivity:
Assume ![]() be an arbitrary element of
be an arbitrary element of ![]()
![]() , which is not equal to 1
, which is not equal to 1
![]()
Therefore, ![]() is not reflexive.
is not reflexive.
Symmetric:
Assume ![]() and
and ![]() , such that
, such that ![]()
![]()
![]() (As addition is commutative)
(As addition is commutative) ![]()
Therefore, ![]() is symmetric.
is symmetric.
Non-Transitivity:
Assume ![]() and
and ![]() , such that
, such that ![]() and
and ![]()
![]() and
and ![]()
On adding both the equation, we obtain
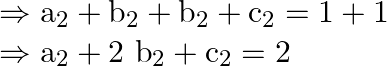
![]() , which is not equal to 1
, which is not equal to 1
![]()
Therefore, ![]() is not transitive.
is not transitive.
As a result, ![]() is symmetric but neither transitive nor reflexive.
is symmetric but neither transitive nor reflexive.
