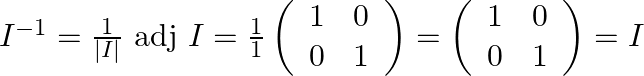Solution:
(i) We need to compute ![]() :
:
We have 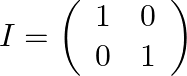
Find: the adjoint of the given matrix.
Step: 1 Find the minor matrix of ![]() .
.
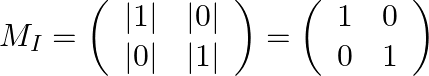
Step: 2 Find the co-factor matrix of ![]() .
.
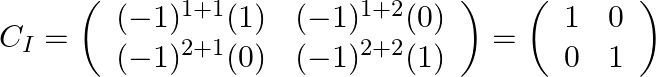
Step: 3 By transpose of ![]() we will have
we will have ![]() .
.
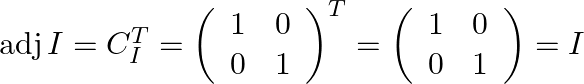
(ii) We need to compute adj ![]() :
:
We have 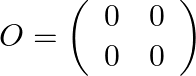
Find: the adjoint of the given matrix.
Step: 1 Find the minor matrix of ![]() .
.
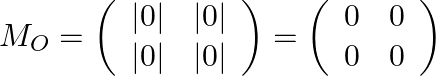
Step: 2 Find the co-factor matrix of ![]() .
.
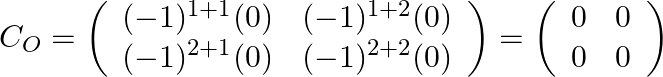
Step: 3 By transpose of ![]() we will have
we will have ![]() .
.
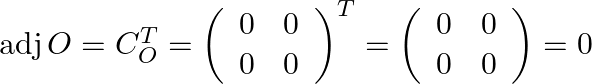
(iii) We need to compute ![]() :
:
We have 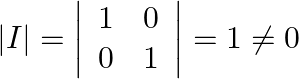 so inverse of given matrix exist.
so inverse of given matrix exist.
The inverse of given matrix is