Login/Sign Up
Home » Prove that the internal bisector of an angle of a triangle divides the opposite side internally in the ratio of the sides containing the angle.
Prove that the internal bisector of an angle of a triangle divides the opposite side internally in the ratio of the sides containing the angle.
CBSE | Class 10 | Exercise-Formative Assessment | Maths | RS Aggarwal | Triangles
Prove that the internal bisector of an angle of a triangle divides the opposite side internally in the ratio of the sides containing the angle.

Answer:

 

 

 

 

 

Let the triangle be ABC with AD as the bisector of ∠???? which meets BC at D.

Draw CE || DA, meeting BA produced at E.

CE || DA

∠2 = ∠3 (???????????????????????????????????? ????????????????????????)

∠1 = ∠4 (???????????????????????????????????????????????????? ????????????????????????)

∠1 = ∠2

∠3 = ∠4

AE = AC

In ∆BCE,

DA || CE.

Applying Thales’ theorem,

\begin{array}{l} \frac{{BD}}{{DC}} = \frac{{AB}}{{AE}}\\ \frac{{BD}}{{DC}} = \frac{{AB}}{{AC}}\\ \end{array}

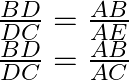
Hence, proved.

i

More Material