Login/Sign Up
Home » Prove the following identities, where the angles involved are acute angles for which the expressions are defined.
Prove the following identities, where the angles involved are acute angles for which the expressions are defined.
CBSE | Class 10 | Introduction to trigonometry | Maths | NCERT
Prove the following identities, where the angles involved are acute angles for which the expressions are defined.

(i) ( cos A–sin A+1)/( cos A +sin A–1) = cosec A + cot A, using the identity cosec2A = 1+cot2A.

(ii)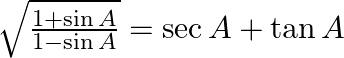\sqrt{\frac{1+\sin A}{1-\sin A}}=\sec A+\tan A

Solutions:

(i) (cos A–sin A+1)/(cos A+sin A–1) = cosec A + cot A, using the identity cosec2A = 1+cot2A.

Using the identity function, cosec2A = 1+cot2A, let’s prove the above equation.

L.H.S. = (cos A–sin A+1)/(cos A+sin A–1)

We get by dividing the numerator and denominator by sin A.

= (cos A–sin A+1)/sin A/(cos A+sin A–1)/sin A

We are aware that cos A/sin A = cot A and 1/sin A = cosec A

= (cot A – 1 + cosec A)/(cot A+ 1 – cosec A)

= (cot A – cosec2A + cot2A + cosec A)/(cot A+ 1 – cosec A) (using cosec2A – cot2A = 1

= [(cot A + cosec A) – (cosec2A – cot2A)]/(cot A+ 1 – cosec A)

= [(cot A + cosec A) – (cosec A + cot A)(cosec A – cot A)]/(1 – cosec A + cot A)

=  (cot A + cosec A)(1 – cosec A + cot A)/(1 – cosec A + cot A)

=  cot A + cosec A = R.H.S.

As a result, (cos A–sin A+1)/(cos A+sin A–1) = cosec A + cot A

Hence Proved.

(ii) 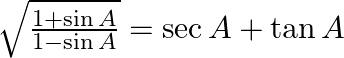\sqrt{\frac{1+\sin A}{1-\sin A}}=\sec A+\tan A

L.H.S.=\sqrt{\frac{1+\sin A}{1-\sin A}}

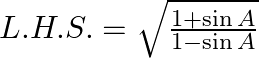
L.H.S. numerator and denominator are first divided by cos A,

We are aware that, 1/cos A = sec A and sin A/ cos A = tan A so it becomes,

= √(sec A+ tan A)/(sec A-tan A)

Now, with the help of rationalization, we may arrive at

=\sqrt{\frac{\sec A+\tan A}{\sec A-\tan A}}*\sqrt{\frac{\sec A+\tan A}{\sec A+\tan A}}

=\sqrt{\frac{{{(\sec A+\tan A)}^{2}}}{{{\sec }^{2}}A-{{\tan }^{2}}A}}

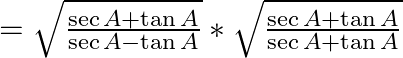
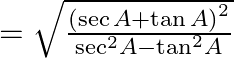
= (sec A + tan A)/1

= sec A + tan A = R.H.S

As a result, hence proved.

i

More Material