Show that each one of the following systems of linear equations is consistent and also find their solutions: (i) 5x + 3y + 7z = 4 3x + 26y + 2z = 9 7x + 2y + 10z = 5 (ii) x + y + z = 6 x + 2y + 3z = 14 x + 4y + 7z = 30

Show that each one of the following systems of linear equations is consistent and also find their solutions:
(i) 5x + 3y + 7z = 4
3x + 26y + 2z = 9
7x + 2y + 10z = 5
(ii) x + y + z = 6
x + 2y + 3z = 14
x + 4y + 7z = 30

Solution:

(i) Given that $5 x+3 y+7 z=4$
$\begin{array}{l} 3 x+26 y+2 z=9 \\ 7 x+2 y+10 z=5 \end{array}$
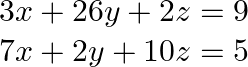
We can write this as:
$\begin{array}{l} {\left[\begin{array}{ccc} 5 & 3 & 7 \\ 3 & 26 & 2 \\ 7 & 2 & 10 \end{array}\right]\left[\begin{array}{l} \mathrm{x} \\ \mathrm{y} \\ \mathrm{z} \end{array}\right]=\left[\begin{array}{l} 4 \\ 9 \\ 5 \end{array}\right]} \\ |\mathrm{A}|=5(260-4)-3(30-14)+7(6-182) \\ =5(256)-3(16)+7(176) \\ |\mathrm{A}|=0 \end{array}$
Therefore, $\mathrm{A}$ is singular. Hence, the given system is either inconsistent or it is consistent with infinitely many solution according to as:
$(\operatorname{Adj} A) \times B \neq 0$ or $(A d j A) \times B=0$
Cofactors of $\mathrm{A}$ are
$\begin{array}{l} C_{11}=(-1)^{1+1} 260-4=256 \\ C_{21}=(-1)^{2+1} 30-14=-16 \\ C_{31}=(-1)^{3+1} 6-182=-176 \\ C_{12}=(-1)^{1+2} 30-14=-16 \\ C_{22}=(-1)^{2+1} 50-49=1 \\ C_{32}=(-1)^{3+1} 10-21=11 \\ C_{13}=(-1)^{1+2} 6-182=-176 \\ C_{23}=(-1)^{2+1} 10-21=11 \\ C_{33}=(-1)^{3+1} 130-9=121 \\ \quad \operatorname{Adj} A=\left[\begin{array}{ccc} 256 & -16 & -176 \\ -16 & 1 & 11 \\ -176 & 11 & 121 \end{array}\right]^{\mathrm{T}} \\ =\left[\begin{array}{ccc} 256 & -16 & -176 \\ -16 & 1 & 11 \\ -176 & 11 & 121 \end{array}\right] \end{array}$
$\operatorname{Adj} A \times B=\left[\begin{array}{ccc}256 & -16 & -176 \\ -16 & 1 & 11 \\ -176 & 11 & 121\end{array}\right]\left[\begin{array}{l}4 \\ 9 \\ 5\end{array}\right]=\left[\begin{array}{l}0 \\ 0 \\ 0\end{array}\right]$
Now, AX = B has infinite many solution
Suppose $z=k$
Therefore, $5 x+3 y=4-7 k$
$3 x+26 y=9-2 k$
We can write this as
$\begin{array}{l} {\left[\begin{array}{cc} 5 & 3 \\ 3 & 26 \end{array}\right]\left[\begin{array}{l} \mathrm{x} \\ \mathrm{y} \end{array}\right]=\left[\begin{array}{l} 4-7 \mathrm{k} \\ 9-2 \mathrm{k} \end{array}\right]} \\ |\mathrm{A}|=121 \end{array}$
$\operatorname{Adj} A=\left[\begin{array}{cc}26 & -3 \\ -3 & 5\end{array}\right]$
Now, $X=A^{-1} B=\frac{1}{|A|}$ Adj $A \times B$
$\begin{array}{l} =\frac{1}{121}\left[\begin{array}{cc} 26 & -3 \\ -3 & 5 \end{array}\right]\left[\begin{array}{l} 4-7 \mathrm{k} \\ 9-2 \mathrm{k} \end{array}\right] \\ =\frac{1}{121}\left[\begin{array}{l} 77-176 \mathrm{k} \\ 11 \mathrm{k}+33 \end{array}\right] \\ {\left[\begin{array}{l} \mathrm{x} \\ \mathrm{y} \\ \mathrm{z} \end{array}\right]=\left[\begin{array}{c} \frac{7-16 \mathrm{k}}{11} \\ \frac{\mathrm{k}+3}{11} \end{array}\right]} \end{array}$
There values of $x, y$ and $z$ satisfy the third equation

(ii) Given that $x+y+z=6$
$\begin{array}{l} x+2 y+3 z=14 \\ x+4 y+7 z=30 \end{array}$
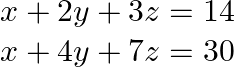
We can write this as:
$\begin{array}{l} {\left[\begin{array}{lll} 1 & 1 & 1 \\ 1 & 2 & 3 \\ 1 & 4 & 7 \end{array}\right]\left[\begin{array}{l} \mathrm{x} \\ \mathrm{y} \\ \mathrm{z} \end{array}\right]=\left[\begin{array}{c} 6 \\ 14 \\ 30 \end{array}\right]} \\ |\mathrm{A}|=1(2)-1(4)+1(2) \end{array}$
$\begin{array}{l} =2-4+2 \\ |A|=0 \end{array}$
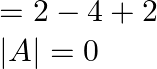
Therefore, A is singular. Hence, the given system is either inconsistent or it is consistent with infinitely many solution according to as:
$(\operatorname{Adj} A) \times B \neq 0$ or $(\operatorname{Adj} A) \times B=0$
Cofactors of A are
$\begin{array}{l} \mathrm{C}_{11}=(-1)^{1+1} 14-12=2 \\ \mathrm{C}_{21}=(-1)^{2+1} 7-4=-3 \\ C_{31}=(-1)^{3+1} 3-2=1 \\ C_{12}=(-1)^{1+2} 7-3=-4 \\ C_{22}=(-1)^{2+1} 7-1=6 \\ C_{32}=(-1)^{3+1} 3-1=2 \\ C_{13}=(-1)^{1+2} 4-2=2 \\ C_{23}=(-1)^{2+1} 4-1=-3 \\ C_{33}=(-1)^{3+1} 2-1=1 \end{array}$
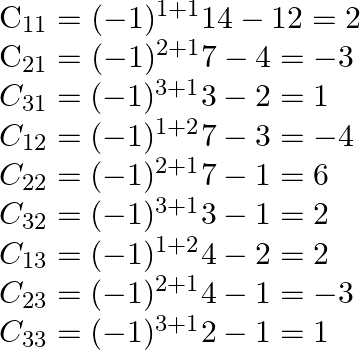
$\operatorname{Adj} A=\left[\begin{array}{ccc}2 & -4 & 2 \\ -3 & 6 & -3 \\ 1 & -2 & 1\end{array}\right]^{\mathrm{T}}$
$=\left[\begin{array}{ccc} 2 & -3 & 1 \\ -4 & 1 & -2 \\ 2 & -3 & 1 \end{array}\right]$
Adj $A \times B=\left[\begin{array}{ccc}2 & -3 & 1 \\ -4 & 1 & -2 \\ 2 & -3 & 1\end{array}\right]\left[\begin{array}{c}6 \\ 14 \\ 30\end{array}\right]=\left[\begin{array}{l}0 \\ 0 \\ 0\end{array}\right]$
Now, $A X=B$ has infinite many solution
Suppose $z=k$
Therefore, $x+y=6-k$
$x+2 y=14-3 k$
We can write this as:
$\left[\begin{array}{ll} 1 & 1 \\ 1 & 2 \end{array}\right]\left[\begin{array}{l} \mathrm{x} \\ \mathrm{y} \end{array}\right]=\left[\begin{array}{c} 6-\mathrm{k} \\ 14-3 \mathrm{k} \end{array}\right]$
$\begin{array}{l} |\mathrm{A}|=1 \\ \text { Adj } \mathrm{A}=\left[\begin{array}{cc} 2 & -1 \\ -1 & 1 \end{array}\right] \end{array}$
Now, $X=A^{-1} B=\frac{1}{|A|}$ Adj $A \times B$
$\begin{array}{r} =\frac{1}{1}\left[\begin{array}{cc} 2 & -1 \\ -1 & 1 \end{array}\right]\left[\begin{array}{c} 6-k \\ 14-3 k \end{array}\right] \\ =\frac{1}{1}\left[\begin{array}{l} 12-2 \mathrm{k}-14+3 \mathrm{k} \\ -6+\mathrm{k}+14-3 \mathrm{k} \end{array}\right] \\ {\left[\begin{array}{l} x \\ y \\ z \end{array}\right]=\left[\begin{array}{c} -2+k \\ 8-2 k \end{array}\right]} \end{array}$
There values of $x, y$ and z satisfy the third equation
As a result, $x=k-2, y=8-2 k, z=k$