Solution:
Given that ![]()
By differentiating the given equation with respect to ![]() , we obtain
, we obtain
![]()
![]()
![]()
Taking different region from ![]()
Suppose ![]()
![]()
![]()
Therefore ![]() is decreasing in
is decreasing in ![]()
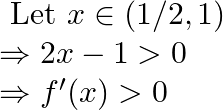
Therefore ![]() is increasing in
is increasing in ![]()
Thus, from above condition we need to find that
![]() is decreasing in
is decreasing in ![]() and increasing in
and increasing in ![]()
As a result, condition for ![]() neither increasing nor decreasing in
neither increasing nor decreasing in ![]()
