Solution:
(i) Given that ![]()
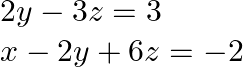
We can write the given system in matrix form as:
![Rendered by QuickLaTeX.com \left[\begin{array}{rrr} 2 & 1 & 1 \\ 1 & 3 & -1 \\ 3 & 1 & -2 \end{array}\right]\left[\begin{array}{l} \mathrm{x} \\ \mathrm{y} \\ \mathrm{Z} \end{array}\right]=\left[\begin{array}{l} 2 \\ 5 \\ 6 \end{array}\right] \text { Or } \mathrm{A} \mathrm{X}=\mathrm{B}](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-9a9581c910e2b4515e7c3ccbea728e4a_l3.png)
![Rendered by QuickLaTeX.com A=\left[\begin{array}{ccc}2 & 1 & 1 \\ 1 & 3 & -1 \\ 3 & 1 & -2\end{array}\right], X=\left[\begin{array}{l}\mathrm{x} \\ \mathrm{y} \\ \mathrm{z}\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-381714e1b292673465e72cf49cba3c34_l3.png) and
and ![Rendered by QuickLaTeX.com \mathrm{B}=\left[\begin{array}{l}2 \\ 5 \\ 6\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-0860b86e847769543091f54fbf340ac8_l3.png)
Now, 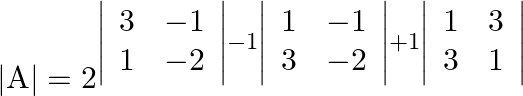
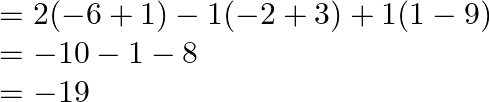
Therefore, the above system of equations has a unique solution, given by
![]()
Cofactors of A are
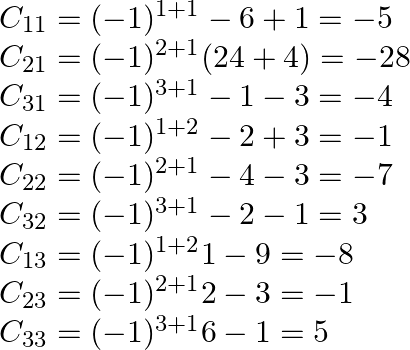
![Rendered by QuickLaTeX.com \begin{array}{l} \text { Adj } A=\left[\begin{array}{ccc} -5 & -1 & -8 \\ 3 & -7 & 1 \\ -4 & 3 & 5 \end{array}\right]^{T} \\ =\left[\begin{array}{ccc} -5 & 3 & -4 \\ -1 & -7 & 3 \\ -8 & 1 & 5 \end{array}\right] \end{array}](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-565b75b6ee6d8aeb637e40e6da497930_l3.png)
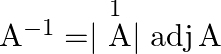
Now, ![Rendered by QuickLaTeX.com X=A^{-1} B=\frac{1}{-19}\left[\begin{array}{ccc}-5 & 3 & -4 \\ -1 & -7 & 3 \\ -8 & 1 & 5\end{array}\right]\left[\begin{array}{l}2 \\ 5 \\ 6\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-76e3d6c6c7a0d9e445f4e57ed1f1d3b4_l3.png)
![Rendered by QuickLaTeX.com \begin{array}{l} X=^{\frac{1}{-19}}\left[\begin{array}{c} -10+15-24 \\ -2-35+18 \\ -16+5+30 \end{array}\right] \\ X=^{\frac{1}{-19}}\left[\begin{array}{c} -19 \\ -19 \\ 19 \end{array}\right] \\ X=\left[\begin{array}{c} 1 \\ 1 \\ -1 \end{array}\right] \end{array}](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-fb417e84759e09899bc4c32c76ad5f6b_l3.png)
As a result, ![]() and
and ![]()
(ii) Given that ![]()
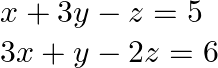
We can write the given system in matrix form as:
![Rendered by QuickLaTeX.com \left[\begin{array}{ccc} 2 & 1 & 1 \\ 1 & 3 & -1 \\ 3 & 1 & -2 \end{array}\right]\left[\begin{array}{l} \mathrm{x} \\ \mathrm{y} \\ \mathrm{z} \end{array}\right]=\left[\begin{array}{l} 2 \\ 5 \\ 6 \end{array}\right]_{\text {Or } A \mathrm{X}=\mathrm{B}}](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-500c0133417ffb1824244c347f085edd_l3.png)
![Rendered by QuickLaTeX.com A=\left[\begin{array}{ccc}2 & 1 & 1 \\ 1 & 3 & -1 \\ 3 & 1 & -2\end{array}\right], X=\left[\begin{array}{l}x \\ y \\ z\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-bbcc209a063e5386f1b1197b0c03e5c4_l3.png) and
and ![Rendered by QuickLaTeX.com B=\left[\begin{array}{l}2 \\ 5 \\ 6\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-302cddeed45e5b562806ed4a8ca4c472_l3.png)
Now, 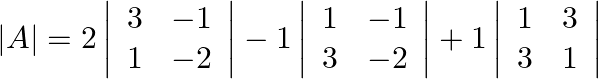
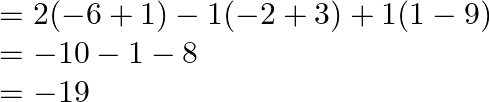
Therefore, the above system of equations has a unique solution, given by
![]()
Cofactors of ![]() are
are
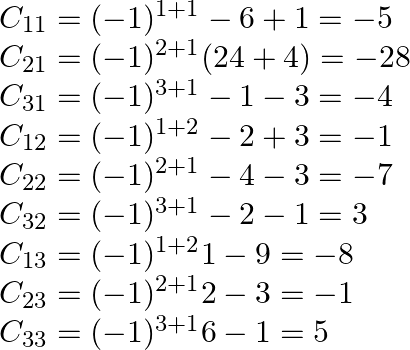
![Rendered by QuickLaTeX.com \begin{array}{l} \text { Adj } A=\left[\begin{array}{ccc} -5 & -1 & -8 \\ 3 & -7 & 1 \\ -4 & 3 & 5 \end{array}\right]^{T} \\ =\left[\begin{array}{ccc} -5 & 3 & -4 \\ -1 & -7 & 3 \\ -8 & 1 & 5 \end{array}\right] \\ A^{-1}=\frac{1}{|A|} a d j A \end{array}](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-3459e50b5d04265ad9569da0efd9e93f_l3.png)
Now, ![Rendered by QuickLaTeX.com X=A^{-1} B=\frac{1}{-19}\left[\begin{array}{ccc}-5 & 3 & -4 \\ -1 & -7 & 3 \\ -8 & 1 & 5\end{array}\right]\left[\begin{array}{l}2 \\ 5 \\ 6\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-76e3d6c6c7a0d9e445f4e57ed1f1d3b4_l3.png)
![Rendered by QuickLaTeX.com \begin{array}{l} X=\frac{1}{-19}\left[\begin{array}{c} -10+15-24 \\ -2-35+18 \\ -16+5+30 \end{array}\right] \\ X=\frac{1}{-19}\left[\begin{array}{c} -19 \\ -19 \\ 19 \end{array}\right] \end{array}](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-f10c3473d9b9b7ae143f2cdd22d882d4_l3.png)
![Rendered by QuickLaTeX.com \mathrm{X}=\left[\begin{array}{c} 1 \\ 1 \\ -1 \end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-c2e57d0f51eacff9d1076f106da9764a_l3.png)
As a result, ![]() and
and ![]()
