Solution:
(i) Given that ![]() and
and ![]()
We can write the above system of equations as
![Rendered by QuickLaTeX.com \left[\begin{array}{ll} 5 & 7 \\ 4 & 6 \end{array}\right]\left[\begin{array}{l} \mathrm{X} \\ \mathrm{Y} \end{array}\right]=\left[\begin{array}{l} -2 \\ -3 \end{array}\right] \text { Or } \mathrm{AX}=\mathrm{B}](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-080a80d014c24a7ff55c9d70e999b163_l3.png)
Where ![Rendered by QuickLaTeX.com A=\left[\begin{array}{ll}5 & 7 \\ 4 & 6\end{array}\right]_{B}=\left[\begin{array}{l}-2 \\ -3\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-22a3a49ef4bb85642582103371cf6b46_l3.png) and
and ![Rendered by QuickLaTeX.com X=\left[\begin{array}{l}\mathrm{X} \\ \mathrm{Y}\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-aa2518a55f9510817013ce40ab12d5fe_l3.png)
![]()
Therefore, the above system of equations has a unique solution, given by ![]()
Suppose ![]() be the cofactor of
be the cofactor of ![]() in A, then
in A, then
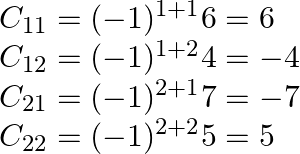
Also, adj ![Rendered by QuickLaTeX.com A=\left[\begin{array}{cc}6 & -4 \\ -7 & 5\end{array}\right]^{\mathrm{T}}](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-5619ac74c159f8cf6cd34baa28506ad6_l3.png)
![Rendered by QuickLaTeX.com \begin{array}{l} =\left[\begin{array}{cc} 6 & -7 \\ -4 & 5 \end{array}\right] \\ A^{-1}=\frac{1}{|\mathrm{~A}|} \operatorname{adj} \mathrm{A} \\ A^{-1}=\frac{1}{2}\left[\begin{array}{cc} 6 & -7 \\ -4 & 5 \end{array}\right] \end{array}](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-8e9e24bd427314e53ff4ccce1d3a39db_l3.png)
Now, ![]()
![Rendered by QuickLaTeX.com \begin{array}{l} {\left[\begin{array}{l} \mathrm{X} \\ \mathrm{Y} \end{array}\right]=\frac{1}{2}\left[\begin{array}{cc} 6 & -7 \\ -4 & 5 \end{array}\right]\left[\begin{array}{l} -2 \\ -3 \end{array}\right]} \\ {\left[\begin{array}{l} \mathrm{X} \\ \mathrm{Y} \end{array}\right]=\frac{1}{2}\left[\begin{array}{c} -12+21 \\ 8-15 \end{array}\right]} \\ {\left[\begin{array}{l} \mathrm{X} \\ \mathrm{Y} \end{array}\right]=\left[\begin{array}{c} \frac{9}{2} \\ \frac{-7}{2} \end{array}\right]} \end{array}](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-6dab55451745dfc1652e852f39edbf11_l3.png)
As a result, ![]() and
and ![]()
(ii) Given that ![]()
![]()
We can write the above system of equations as
![]()
Where ![Rendered by QuickLaTeX.com A=\left[\begin{array}{ll}5 & 2 \\ 3 & 2\end{array}\right]_{B}=\left[\begin{array}{l}3 \\ 5\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-fecb85096c773ff355cd911603d30a16_l3.png) and
and ![Rendered by QuickLaTeX.com X=\left[\begin{array}{l}\mathrm{X} \\ \mathrm{Y}\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-aa2518a55f9510817013ce40ab12d5fe_l3.png)
![]()
Therefore, the above system of equations has a unique solution, given by
![]()
Suppose ![]() be the cofactor of
be the cofactor of ![]() in
in ![]() , then
, then
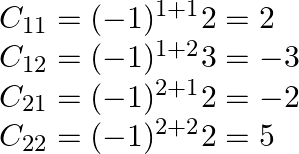
Also, adj ![Rendered by QuickLaTeX.com A=\left[\begin{array}{cc}2 & -3 \\ -2 & 5\end{array}\right]^{\mathrm{T}}](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-b24ed219656835da45b76fc6c9791585_l3.png)
![Rendered by QuickLaTeX.com \begin{array}{l} =\left[\begin{array}{cc} 2 & -2 \\ -3 & 5 \end{array}\right] \\ A^{-1}=\frac{1}{|A|} \operatorname{adj} A \\ A^{-1}=\frac{1}{4}\left[\begin{array}{cc} 2 & -2 \\ -3 & 5 \end{array}\right] \end{array}](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-8d9685d396ed7829b69653be4d79520f_l3.png)
Now, ![]()
![Rendered by QuickLaTeX.com \begin{array}{l} {\left[\begin{array}{l} \mathrm{X} \\ \mathrm{Y} \end{array}\right]=\frac{1}{4}\left[\begin{array}{cc} 2 & -2 \\ -3 & 5 \end{array}\right]\left[\begin{array}{l} 3 \\ 5 \end{array}\right]} \\ {\left[\begin{array}{l} \mathrm{X} \\ \mathrm{Y} \end{array}\right]=\frac{1}{4}\left[\begin{array}{c} 6-10 \\ -9+25 \end{array}\right]} \\ {\left[\begin{array}{l} \mathrm{X} \\ \mathrm{Y} \end{array}\right]=\frac{1}{4}\left[\begin{array}{l} -4 \\ 16 \end{array}\right]} \\ {\left[\begin{array}{l} \mathrm{X} \\ \mathrm{Y} \end{array}\right]=\left[\begin{array}{c} -1 \\ 4 \end{array}\right]} \end{array}](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-5b97fef7b570a0dfa6bfe267f0494a51_l3.png)
As a result, ![]() and
and ![]()
