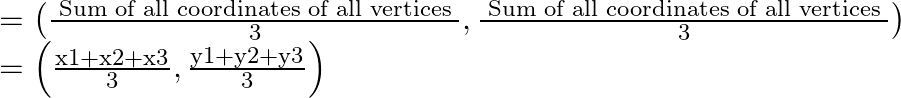Solution:
(i) Let (p, q) be the coordinates of a point Q.
Provided,
The point Q (p, q),
Divide the line joining 
and 
in the ratio 
, Then,
Coordinates of 
![\begin{array}{l} {\left[\frac{2 \times\left(\frac{\mathrm{x}{1}+\mathrm{x}{3}}{2}\right)+1 \times \mathrm{x}{2}}{2+1}, \frac{2 \times\left(\frac{\mathrm{y}{1}+\mathrm{y}{3}}{2}\right)+1 \times \mathrm{y}{2}}{2+1}\right]} \\ =\left(\frac{\mathrm{x}{1}+\mathrm{x}{2}+\mathrm{x}{3}}{3}, \frac{\mathrm{y}{1}+\mathrm{y}{2}+\mathrm{y}{3}}{3}\right) \end{array}](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-5da1c4d4a9a24625eb918c6baf8ed1ff_l3.png "Rendered by QuickLaTeX.com")
As, BE is the median of side CA, as a result BE divides AC in to two equal halves. As a result the mid-point of 
Coordinate of 
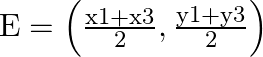
Therefore, the required coordinate of point 
;
Now,
Let the coordinates of a point E be (⍺, β)
Given,
Point 
divide the line joining 
and 
in the ratio
Then the coordinates of 
![\begin{array}{l} =\left[\frac{2 \times\left(\frac{\mathrm{x}{1}+\mathrm{x}{2}}{2}\right)+1 \times \mathrm{x}{3}}{2+1}, \frac{2 \times\left(\frac{\mathrm{y}{1}+\mathrm{y}{2}}{2}\right)+1 \times \mathrm{y}{3}}{2+1}\right] \\ =\left(\frac{\mathrm{x}{1}+\mathrm{x}{2}+\mathrm{x}{3}}{3}, \frac{\mathrm{y}{1}+\mathrm{y}{2}+\mathrm{y}{3}}{3}\right) \end{array}](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-1f106cc97faf937d8930e9e12d3919c1_l3.png "Rendered by QuickLaTeX.com")
As, 
is the median of side 
.
Therefore, CF divides in to two equal halves. 
mid-point of 
Coordinate of 
As a result, the required coordinate of point 
;
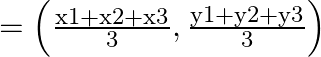
(ii) Coordinate of the ΔABC’s centroid ;
