Solution:
Given: ![]()
![]()
Position vector of ![]() which divides
which divides ![]() in the ratio
in the ratio ![]() externally is given by
externally is given by
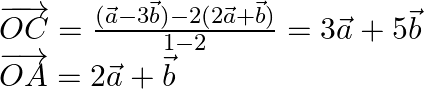
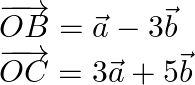
If A is mid-point, then
OA can also be given by 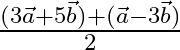
![]() Which is true
Which is true
Hence A is mid-point of CB
Solution:
Given: ![]()
![]()
Position vector of ![]() which divides
which divides ![]() in the ratio
in the ratio ![]() externally is given by
externally is given by
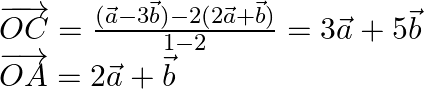
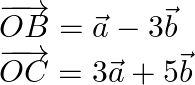
If A is mid-point, then
OA can also be given by 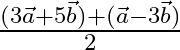
![]() Which is true
Which is true
Hence A is mid-point of CB