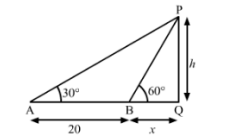
Let ![]() be the height of the
be the height of the ![]() tower and
tower and ![]() be the width of the canal. We have,
be the width of the canal. We have,
![]() and
and ![]()
In ![]()
![]()
![]()
![]()
Again in ![]()
![]()
![]()
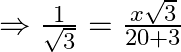
![]()
![]()
![]()
![]()
![]()
Substituting ![]() in (i), we get
in (i), we get
![]()
=> the height of the TV tower is ![]() and the width of the canal is
and the width of the canal is ![]() .
.

Let ![]() be the height of the
be the height of the ![]() tower and
tower and ![]() be the width of the canal. We have,
be the width of the canal. We have,
![]() and
and ![]()
In ![]()
![]()
![]()
![]()
Again in ![]()
![]()
![]()
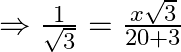
![]()
![]()
![]()
![]()
![]()
Substituting ![]() in (i), we get
in (i), we get
![]()
=> the height of the TV tower is ![]() and the width of the canal is
and the width of the canal is ![]() .
.