Login/Sign Up
Home » ABCD is a parallelogram in which P is the midpoint of DC and Q is a point on AC such that CQ = AC. If PQ produced meets BC at R, prove that R is the midpoint of BC.
ABCD is a parallelogram in which P is the midpoint of DC and Q is a point on AC such that CQ = \begin{array}{l} \frac{{1}}{{4}} \end{array} AC. If PQ produced meets BC at R, prove that R is the midpoint of BC.
CBSE | Class 10 | Exercise 4A | Maths | RS Aggarwal | Triangles
ABCD is a parallelogram in which P is the midpoint of DC and Q is a point on AC such that CQ = \begin{array}{l} \frac{{1}}{{4}} \end{array} AC. If PQ produced meets BC at R, prove that R is the midpoint of BC.

Answer:

 

 

 

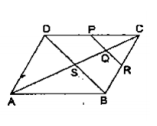
We know that the diagonals of a parallelogram bisect each other.

Therefore,

CS =  \begin{array}{l} \frac{{1}}{{2}} \end{array}

AC …(i)

Also, it is given that CQ = \begin{array}{l} \frac{{1}}{{4}} \end{array}

AC …(ii)

Dividing equation (ii) by (i),

\begin{array}{l} \frac{{CQ}}{{CS}} = \frac{{\frac{1}{4}AC}}{{\frac{1}{2}AC}}\\ CQ = \frac{1}{2}CS \end{array}

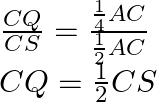
Q is the midpoint of CS

According to midpoint theorem in ∆CSD

PQ || DS

If PQ || DS,

QR || SB

In ∆ CSB, Q is midpoint of CS and QR ‖ SB.

Applying converse of midpoint theorem,

Conclusion – R is the midpoint of CB.

Hence, proved.

i

More Material