
Let ![]() be the lighthouse and
be the lighthouse and ![]() and
and ![]() be the positions of the ship.
be the positions of the ship.
![]() and
and ![]()
![]() and
and ![]()
In the right ![]() , we have
, we have
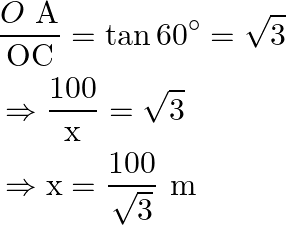
in the right ![]() , we have:
, we have:
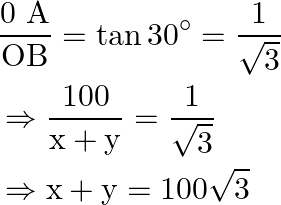
putting ![]() in the above equation, we get:
in the above equation, we get:
![]()
![]() Distance travelled by the ship during the period of observation
Distance travelled by the ship during the period of observation ![]()

Let ![]() be the lighthouse and
be the lighthouse and ![]() and
and ![]() be the positions of the ship.
be the positions of the ship.
![]() and
and ![]()
![]() and
and ![]()
In the right ![]() , we have
, we have
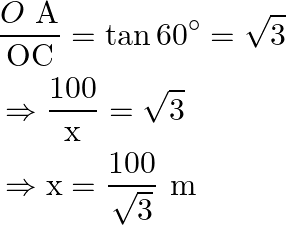
in the right ![]() , we have:
, we have:
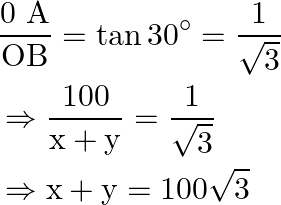
putting ![]() in the above equation, we get:
in the above equation, we get:
![]()
![]() Distance travelled by the ship during the period of observation
Distance travelled by the ship during the period of observation ![]()