Login/Sign Up
Home » Compute AB and BA, which ever exists when
Compute AB and BA, which ever exists when A=\left[\begin{array}{cc} 2 & -1 \\ 3 & 0 \\ -1 & 4 \end{array}\right] \text { and } B=\left[\begin{array}{cc} -2 & 3 \\ 0 & 4 \end{array}\right]
CBSE | Class 12 | Exercise 5C | Maths | Matrices | RS Aggarwal
Compute AB and BA, which ever exists when A=\left[\begin{array}{cc} 2 & -1 \\ 3 & 0 \\ -1 & 4 \end{array}\right] \text { and } B=\left[\begin{array}{cc} -2 & 3 \\ 0 & 4 \end{array}\right]

Solution:

We have 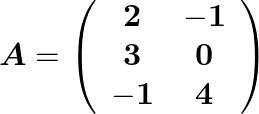\boldsymbol{A}=\left(\begin{array}{cc}\mathbf{2} & \mathbf{- 1} \\ \mathbf{3} & \mathbf{0} \\ \mathbf{- 1} & \mathbf{4}\end{array}\right) and \boldsymbol{B}=\left(\begin{array}{cc}-\mathbf{2} & \mathbf{3} \\ \mathbf{0} & \mathbf{4}\end{array}\right).
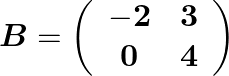Now if number of columns in left matrix is equals to the number of rows in right matrix, multiplication of two matrices is possible.

Now discuss the order of the matrices which are given. The order of matrix \boldsymbol{A} is \mathbf{3} \times \mathbf{2} and matrix \boldsymbol{B} is \mathbf{2} \times \mathbf{2}.
Hence, the multiplications we can proceed as,

(i) The multiplication \boldsymbol{A B} is possible.
Hence 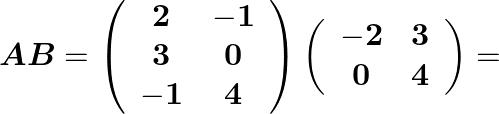\boldsymbol{A B}=\left(\begin{array}{cc}\mathbf{2} & \mathbf{- 1} \\ \mathbf{3} & \mathbf{0} \\ -\mathbf{1} & \mathbf{4}\end{array}\right)\left(\begin{array}{cc}-\mathbf{2} & \mathbf{3} \\ \mathbf{0} & \mathbf{4}\end{array}\right)=
\left(\begin{array}{cc}(2)(-2)+(-1)(0) & (2) 3+(-1) 4 \\ 3(-1)+(0)(0) & (3) 3+(0) 4 \\ (-1)(-2)+(4)(0) & (-1) 3+(4) 4\end{array}\right)=\left(\begin{array}{cc}-4 & 2 \\ -6 & 9 \\ 2 & 13\end{array}\right)

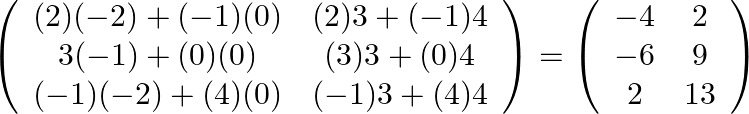
(ii) The multiplication of \boldsymbol{B} \boldsymbol{A} is not possible as if number of columns in left matrix is 2 which is not equals to the number of rows in right matrix i.e, 3 .

i

More Material