Solution:
The function provided is 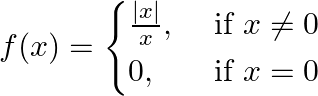
Also the ![]() can be defined as,
can be defined as,
![]()
![]()
Now we know that, the domain of ![]() is
is ![]() as
as ![]() is defined for
is defined for ![]() and
and ![]() . It is constant function and continuous for all
. It is constant function and continuous for all ![]() ,
, ![]() .
.
It is a constant function and continuous for all ![]() .
.
As a result ![]() is continuous on
is continuous on ![]() .
.
Now,
L.H.L.= ![]()
R.H.L.= ![]()
Since, ![]()
As a result, ![]() does not exist and
does not exist and ![]() is discontinuous at only
is discontinuous at only ![]() .
.
