Find the conjugates of the following complex numbers: (i) [(1 + i) (2 + i)] / (3 + i) (ii) [(3 – 2i) (2 + 3i)] / [(1 + 2i) (2

Home » Find the conjugates of the following complex numbers: (i) [(1 + i) (2 + i)] / (3 + i) (ii) [(3 – 2i) (2 + 3i)] / [(1 + 2i) (2 – i)]

Find the conjugates of the following complex numbers:
(i) [(1 + i) (2 + i)] / (3 + i)
(ii) [(3 – 2i) (2 + 3i)] / [(1 + 2i) (2 – i)]

Find the conjugates of the following complex numbers:
(i) [(1 + i) (2 + i)] / (3 + i)
(ii) [(3 – 2i) (2 + 3i)] / [(1 + 2i) (2 – i)]

Solution:

(i) $[(1+i)(2+i)] /(3+i)$
As the given complex no. is not in the standard form of $(a+i b)$
Convert it to standard form,
$\begin{aligned} \frac{(1+i)(2+i)}{3+i} =\frac{1(2+i)+i(2+i)}{3+i} \\ =\frac{2+i+2 i+i^{2}}{3+i} \\ =\frac{2+3 i+(-1)}{3+i}\left[\text { Since, } i^{2}=-1\right] \\ =\frac{1+3 i}{3+i} \end{aligned}$
On multiplying and dividing it with $(3-10)$ we obtain,
$\begin{aligned} \frac{1+3 i}{3+i} =\frac{1+3 i}{3+i} \times \frac{3-i}{3-i} \\ =\frac{1(3-i)+3 i(3-i)}{3^{2}-i^{2}} \\ =\frac{3-i+9 i-3 i^{2}}{9-(-1)}\left[\text { Since }, i^{2}=-1\right] \\ =\frac{3+8 i-3(-1)}{10} \\ =\frac{6+8 i}{10} \\ =\frac{3}{5}+\frac{4 i}{5} \end{aligned}$
It is known that the conjugate of a complex number $(a+i b)$ is $(a - ib)$
As a result, the conjugate of $(3+4 i) / 5$ is $(3-4 i) / 5$

(ii) $[(3-2 \mathrm{i})(2+3 \mathrm{i})] /[(1+2 \mathrm{i})(2-\mathrm{i})]$
As the given complex no. is not in the standard form of $(a +ib)$
Convert it to standard form,
$\begin{aligned} \frac{(3-2 i)(2+3 i)}{(1+2 i)(2-i)} =\frac{3(2+3 i)-2 i(2+3 i)}{1(2-i)+2 i(2-i)} \\ =\frac{6+9 i-4 i-6 i^{2}}{2-i+4 i-2 i^{2}} \\ =\frac{6+5 i-6(-1)}{2+3 i-2(-1)} \\ =\frac{12+5 i}{4+3 i} \end{aligned}$
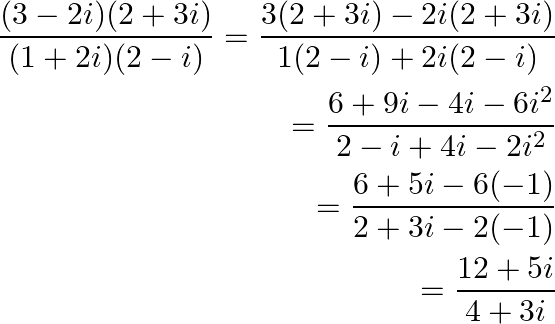
On multiplying and dividing with $(4-3 i)$ we obtain,
$\begin{aligned} \frac{12+5 i}{4+3 i} =\frac{12+5 i}{4+3 i} \times \frac{4-3 i}{4-3 i} \\ =\frac{12(4-3 i)+5 i(4-3 i)}{4^{2}-(3 i)^{2}} \\ =\frac{48-36 i+20 i-15 i^{2}}{16-9 i^{2}} \\ =\frac{48-16 i-15(-1)}{16-9(-1)} \\ =\frac{63-16 i}{25} \end{aligned}$
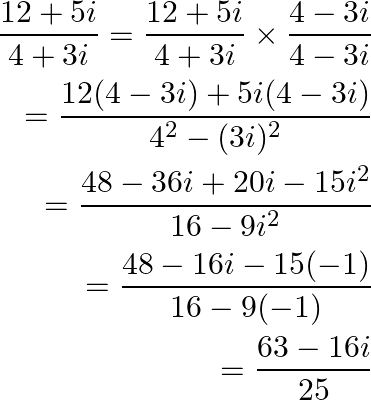
It is known that the conjugate of a complex number $(a + ib)$ is $(a - ib)$