We realize that condition of the line making blocks an and b on x-and y-axis, individually, is
![]()
Given: amount of captures = 9
![]()
![]()
Presently, substitute worth of b in the above condition, we get
![]()
Given: the line goes through the point (2, 2),
In this way,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
After factorizing, we get
![]()
![]()
![]()
![]()
Allow us to substitute in (1),
![]()
Then, at that point,
![]()
![]()
![]()
![]()
![]()
Then, at that point,
![]()
![]()
![]()
![]()
∴ The condition of the line is
![]()

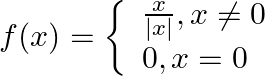 . Show that
. Show that 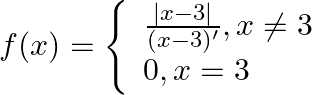 . Show that
. Show that