Solution:
(i) The criteria of existence of inverse matrix is the determinant of a given matrix should not be equal to zero.
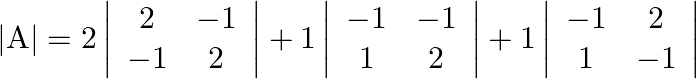
![]()
![]()
![]()
Thus, ![]() exists
exists
Cofactors of ![]() are
are
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
It is known that adj ![Rendered by QuickLaTeX.com A=\left[\begin{array}{lll}C_{11} & C_{12} & C_{13} \\ C_{21} & C_{22} & C_{23} \\ C_{31} & C_{32} & C_{33}\end{array}\right]^{T}](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-2d371211c5015cd081588d70ba897496_l3.png)
![Rendered by QuickLaTeX.com =\left[\begin{array}{ccc}3 & 1 & -1 \\ 1 & 3 & 1 \\ -1 & 1 & 3\end{array}\right]^{\mathrm{T}}](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-e20bb0f67f92a5b144e5453d318404f8_l3.png)
Therefore, adj ![Rendered by QuickLaTeX.com A=\left[\begin{array}{ccc}3 & 1 & -1 \\ 1 & 3 & 1 \\ -1 & 1 & 3\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-68bccce7c41878a74b9bd0a140ac2277_l3.png)
Now, ![]() adj
adj ![]()
Therefore, ![Rendered by QuickLaTeX.com A^{-1}=\frac{1}{4}\left[\begin{array}{ccc}3 & 1 & -1 \\ 1 & 3 & 1 \\ -1 & 1 & 3\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-738567b8b2a8a64c42ff916dce3cf98a_l3.png)
Thus, ![Rendered by QuickLaTeX.com A^{-1}=\left[\begin{array}{ccc}\frac{3}{4} & \frac{1}{4} & \frac{-1}{4} \\ \frac{1}{4} & \frac{3}{4} & \frac{1}{4} \\ \frac{-1}{4} & \frac{1}{4} & \frac{1}{4}\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-553b5045fdb5dc8968a4f0d7c627af08_l3.png)
(ii) The criteria of existence of inverse matrix is the determinant of a given matrix should not be equal to zero.
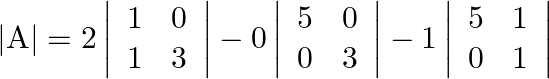
![]()
![]()
![]()
Thus, ![]() exists
exists
Cofactors of ![]() are
are
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \begin{array}{l} C_{22}=6 \\ C_{32}=-5 \\ C_{13}=5 \\ C_{23}=-2 \\ C_{33}=2 \\ \text { It is known that adj } A=\left[\begin{array}{ccc} C_{11} & C_{12} & C_{13} \\ C_{21} & C_{22} & C_{23} \\ C_{31} & C_{32} & C_{33} \end{array}\right]^{T} \\ \text { Therefore, } \operatorname{adj} A=\left[\begin{array}{ccc} 3 & -1 & 1 \\ -15 & 6 & -5 \\ 5 & -2 & 2 \end{array}\right] \\ \text { Now, } A^{-1}=\frac{1}{|A|} \operatorname{adj} A \\ \text { Therefore, } A^{-1}=\frac{1}{1}\left[\begin{array}{ccc} 3 & -1 & 1 \\ -15 & 6 & -5 \\ 5 & -2 & 2 \end{array}\right] \\ =\left[\begin{array}{ccc} 3 & -15 & 5 \\ -1 & 6 & -2 \\ 1 & -5 & 2 \end{array}\right]^{\mathrm{T}} \\ =\left[\begin{array}{ccc} -15 & 6 & -5 \\ 5 & -2 & 2 \end{array}\right] \end{array}](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-560feaf68e94d2cc523472f827b8bb62_l3.png)

![Rendered by QuickLaTeX.com \begin{aligned} &\text { (i) } \left.\begin{array}{ccc} -1 & 2 & -1 \\ 1 & -1 & 2 \end{array}\right] \\ \end{aligned}](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-36da389963752f03270e494a9396201a_l3.png)
![Rendered by QuickLaTeX.com \begin{aligned} &(ii)\left[\begin{array}{ccc} 2 & 0 & -1 \\ 5 & 1 & 0 \\ 0 & 1 & 3 \end{array}\right] \\ \end{aligned}](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-c2865b219ba3bdefff56820f47a0448f_l3.png)