Solution:
(i) The criteria of existence of inverse matrix is the determinant of a given matrix should not be equal to zero.
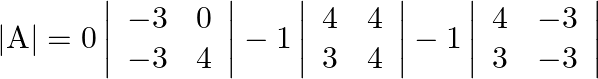
![]()
![]()
![]()
Thus, ![]() exists
exists
Cofactors of ![]() are
are
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
It is known that adj ![Rendered by QuickLaTeX.com A=\left[\begin{array}{lll}C_{11} & C_{12} & C_{13} \\ C_{21} & C_{22} & C_{23} \\ C_{31} & C_{32} & C_{33}\end{array}\right]^{T}](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-2d371211c5015cd081588d70ba897496_l3.png)
![Rendered by QuickLaTeX.com =\left[\begin{array}{ccc}0 & -4 & -3 \\ -1 & 3 & 3 \\ 1 & -4 & -4\end{array}\right]^{\mathrm{T}}](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-1f9f39fe3a480989e83c7ff828dcb057_l3.png)
Therefore, adj ![Rendered by QuickLaTeX.com A=\left[\begin{array}{ccc}0 & -1 & 1 \\ -4 & 3 & -4 \\ -3 & 3 & -4\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-29465086d7deaa004ad14323d4a87cd7_l3.png)
Now, ![]()
Therefore, ![Rendered by QuickLaTeX.com A^{-1}=\frac{1}{-1}\left[\begin{array}{ccc}0 & -1 & 1 \\ -4 & 3 & -4 \\ -3 & 3 & -4\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-75dafde3300fa7eda2b7c0ebd815feb7_l3.png)
Thus, ![Rendered by QuickLaTeX.com \mathrm{A}^{-1}=\left[\begin{array}{ccc}0 & 1 & -1 \\ 4 & -3 & 4 \\ 3 & -3 & 4\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-66ad05bce3ac33e98738366dfd42c60f_l3.png)
(ii) The criteria of existence of inverse matrix is the determinant of a given matrix should not be equal to zero.
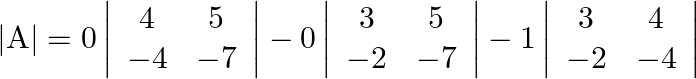
![]()
![]()
Thus, ![]() exists
exists
Cofactors of ![]() are
are
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
It is known that adj ![Rendered by QuickLaTeX.com A=\left[\begin{array}{lll}C_{11} & C_{12} & C_{13} \\ C_{21} & C_{22} & C_{23} \\ C_{31} & C_{32} & C_{33}\end{array}\right]^{\mathrm{T}}](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-6a9385b25da8e79501b00d40eb3af8b5_l3.png)
![Rendered by QuickLaTeX.com =\left[\begin{array}{ccc}8 & 11 & -4 \\ 4 & -2 & 0 \\ 4 & -3 & 0\end{array}\right]^{\mathrm{T}}](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-f27687833506e1029c42cf07b11d3755_l3.png)
Therefore, ![Rendered by QuickLaTeX.com \operatorname{adj} \mathrm{A}=\left[\begin{array}{ccc}8 & 4 & 4 \\ 11 & -2 & -3 \\ -4 & 0 & 0\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-5d861768391f2dde73d5f5030fc7b2da_l3.png)
Now, ![]()
Therefore, ![Rendered by QuickLaTeX.com A^{-1}=\frac{1}{4}\left[\begin{array}{ccc}8 & 4 & 4 \\ 11 & -2 & -3 \\ -4 & 0 & 0\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-89b9af95d532f0f61263521794560f3c_l3.png)
Thus, ![Rendered by QuickLaTeX.com A^{-1}=\left[\begin{array}{ccc}2 & 1 & 1 \\ \frac{11}{4} & \frac{-1}{2} & \frac{-3}{4} \\ -1 & 0 & 0\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-f9e4b1339603554e3fb33b79d039e4b5_l3.png)

![Rendered by QuickLaTeX.com \begin{aligned} &(i)\left[\begin{array}{ccc} 0 & 1 & -1 \\ 4 & -3 & 4 \\ 3 & -3 & 4 \end{array}\right] \\ \end{aligned}](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-7ec25a09ce208880a4fcbfec74e43028_l3.png)
![Rendered by QuickLaTeX.com \begin{aligned} &(ii)\left[\begin{array}{ccc} 0 & 0 & -1 \\ 3 & 4 & 5 \\ -2 & -4 & -7 \end{array}\right] \end{aligned}](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-033273619afa4c9c4cbaf9e4a039ee19_l3.png)