Login/Sign Up
Home » Find the real values of and , if (i) (ii)
Find the real values of x and y, if
(i) (x+i y)(2-3 i)=4+i
(ii) (3 x-2 i y)(2+i)^{2}=10(1+i)
CBSE | Class 11 | Complex Numbers | Exercise 13.2 | Maths | RD Sharma
Find the real values of x and y, if
(i) (x+i y)(2-3 i)=4+i
(ii) (3 x-2 i y)(2+i)^{2}=10(1+i)

Solution:

(i) (x+i y)(2-3 i)=4+i

On simplifying the expression we obtain,
\begin{array}{l} x(2-3 i)+i y(2-3 i)=4+i \\ 2 x-3 x i+2 y i-3 y i^{2}=4+i \\ 2 x+(-3 x+2 y) i-3 y(-1)=4+i\left[\text { since, } i^{2}=-1\right] \\ 2 x+(-3 x+2 y) i+3 y=4+i\left[\text { since, } i^{2}=-1\right] \\ (2 x+3 y)+i(-3 x+2 y)=4+i \end{array}
Equating the Real and Imaginary parts on both the sides, we obtain
2 x+3 y=4 \ldots \text { (i) }
And -3 x+2 y=1 \ldots (ii)
Multiplying eq.(i) by 3 and eq.(ii) by 2 and add
By solving we obtain,
\begin{array}{l} 6 x-6 x-9 y+4 y=12+2 \\ 13 y=14 \\ y=14 / 13 \end{array}
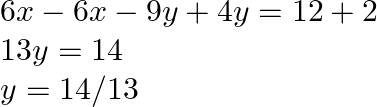
On substituting the value of y in eq.(i) we obtain,
\begin{array}{l} 2 x+3 y=4 \\ 2 x+3(14 / 13)=4 \\ 2 x=4-(42 / 13) \\ =(52-42) / 13 \\ 2 x=10 / 13 \\ x=5 / 13 \end{array}
x=5 / 13, y=14 / 13
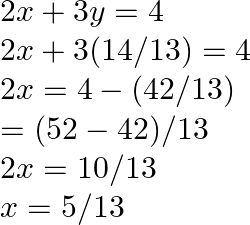
As a result, the real values of x and y are 5 / 13,14 / 13

(ii) (3 x-2 i y)(2+i)^{2}=10(1+i)
Given that
\begin{array}{l} (3 x-2 i y)(2+i)^{2}=10(1+i) \\ (3 x-2 y i)\left(2^{2}+i^{2}+2(2)(i)\right)=10+10 i \\ (3 x-2 y i)(4+(-1)+4 i)=10+10 i\left[\text { since } i^{2}=-1\right] \\ (3 x-2 y i)(3+4 i)=10+10 i \end{array}
On dividing with 3+4 \mathrm{i} on both the sides we obtain,
(3 x-2 y i)=(10+10 i) /(3+4 i)
Multiply and divide with (3-4i)
\begin{array}{l} =[10(3-4 i)+10 i(3-4 i)] /\left(3^{2}-(4 i)^{2}\right) \\ =\left[30-40 i+30 i-40 i^{2}\right] /\left(9-16 i^{2}\right) \\ =[30-10 i-40(-1)] /(9-16(-1)) \\ =[70-10 i] / 25 \end{array}
Equating the Real and Imaginary parts on both the sides we obtain 3 x=70 / 25 and -2 y=-10 / 25
x=70 / 75 \text { and } y=1 / 5
x=14 / 15 \text { and } y=1 / 5
As a result, the real values of x and y are 14 / 15,1 / 5

i

More Material