Solution:

We have and are symmetric matrices. Therefore and
The transpose of the matrix is an operation of making interchange of elements by the rule on positioned element shifted to new position .
The symmetric matrix is defined as similarity of transpose of matrix with it self. i.e, .

The skew-symmetric matrix is defined as similarity of transpose of matrix with it self. i.e, .
We have some properties of transpose of matrices:

(i) (ii)
Let’s check

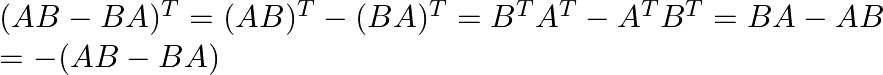
Therefore we are having is skew symmetric.