(i) Consider the nucleus of a H atom as a point charge electron circling about it at a speed of ![]() and a radius of
and a radius of ![]() The Coulombian force acts as a centrifugal force, causing the nucleus to circle.
The Coulombian force acts as a centrifugal force, causing the nucleus to circle.
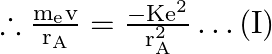
Here ![]()
(-) sign shows the force of attraction.
By Bohr’s postulate, we have angular momentum as ![]()
![]()
![]()
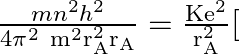 From I
From I ![]()
![]()
For ground state ![]() , we have,
, we have,
![]()
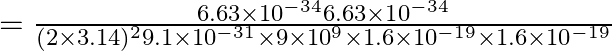
![]()
![]()
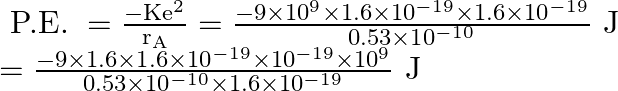
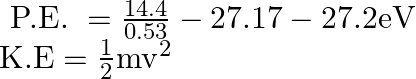
![]() for ground state)
for ground state)
![]()
![]()
![]()
![]()
![]()
(ii) In the case of a spherical nucleus with a radius of ![]() , the electron moves charge within the nucleus
, the electron moves charge within the nucleus ![]() , and then the electron moves inside the nucleus. Then (
, and then the electron moves inside the nucleus. Then ( ![]() is the radius of the rotating electron’s new Bohr’s orbit)
is the radius of the rotating electron’s new Bohr’s orbit)
Charge 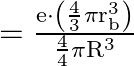
![]()
![]()
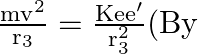 Coulomb’s law
Coulomb’s law ![]()
![]() (By Bohr’s postulate)
(By Bohr’s postulate)
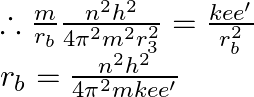
Now for ground state of ![]() and
and 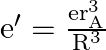 , then we have,
, then we have,
![Rendered by QuickLaTeX.com \therefore \mathrm{r}_{\mathrm{b}}=\frac{\mathrm{h}^{2}}{4 \pi^{2} \mathrm{mK} \cdot \mathrm{e} \cdot \mathrm{e} \cdot \frac{\mathrm{r}_{\mathrm{b}}^{3}}{\mathrm{R}^{3}}}=\left[\frac{\mathrm{h}^{2}}{4 \pi^{2} \mathrm{mK} \mathrm{e}^{2}}\right] \times \frac{\mathrm{R}^{3}}{\mathrm{r}_{\mathrm{b}}^{3}}=\mathrm{r}_{\mathrm{A}} \times \frac{\mathrm{R}^{3}}{\mathrm{r}_{\mathrm{b}}^{3}}](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-4ddc4c8e7640f28ea837586531923cf9_l3.png)
![Rendered by QuickLaTeX.com \begin{array}{l} \left[\because \mathrm{r}_{\mathrm{A}}=\frac{\mathrm{h}^{2}}{4 \pi^{2} \mathrm{mK} \mathrm{e}^{3}}=0.53 \mathrm{~A}^{\circ} \text { calclated in } \operatorname{part}(\mathrm{i})\right]\\ \mathrm{r}_{\mathrm{b}}=\mathrm{r}_{\mathrm{A}}\left[\frac{\mathrm{R}}{\mathrm{r}_{\mathrm{b}}}\right]^{3}\\ \mathrm{r}_{\mathrm{b}}^{4}=\mathrm{r}_{\mathrm{A}} \mathrm{R}^{3}=0.53 \mathrm{~A}^{\circ} \times\left(10 \mathrm{~A}^{\circ}\right)^{3}\\ \mathrm{r}_{\mathrm{b}}^{\mathrm{A}}=0.53 \times 1000\left(\mathrm{~A}^{\circ}\right)^{4}\left(\because \mathrm{r}_{\mathrm{A}}=0.53 \mathrm{~A}^{\circ}\right)\\ \mathrm{r}_{\mathrm{b}}=[530] \frac{1}{4} \mathrm{~A}^{\circ}<\mathrm{RA}^{\circ}\\ \text { K.E. }=\frac{1}{2} m v^{2}=\frac{m}{2} \cdot \frac{h^{2}}{4 \pi^{2} \mathrm{~m}^{2} \mathrm{r}_{\mathrm{b}}^{2}}=\frac{\mathrm{h}^{2}}{8 \pi^{2} \mathrm{mr}_{\mathrm{b}}^{2}}\left[\because \mathrm{v}=\frac{\mathrm{n}^{2} \mathrm{~h}^{2}}{4 \pi^{2} \mathrm{~m}^{2} \mathrm{r}_{\mathrm{b}}^{2}}\right]\\ =\frac{6.62 \times 6.62 \times 10^{-34} \times 10^{-34}}{8 \times 3.14 \times 3.14 \times 9.1 \times 10^{-31} \times 4.8 \times 4.8 \times 10^{-20} \times 1.6 \times 10^{-19}} \mathrm{eV}\\ =\frac{6.62 \times 6.62 \times 10^{-68+31+20+19}}{8 \times 3.14 \times 3.14 \times 9.1 \times 4.8 \times 4.8 \times 1.6} \mathrm{eV}\\ =\frac{43.8244}{26460.2} 10^{-58+70}-0.001656 \times 10^{2} \mathrm{eV}\\ \mathrm{K} . \mathrm{E}=0.167 \mathrm{eV}\\ \mathrm{P} . \mathrm{E} .=\frac{\mathrm{e}^{2}}{4 \pi \varepsilon_{0}} \frac{\left(\mathrm{r}_{\mathrm{b}}^{2}-3 \mathrm{R}^{2}\right)}{\mathrm{R}^{3}}\left[\mathrm{P} \cdot \mathrm{E}=\frac{\mathrm{Kq}_{1} \mathrm{q}_{2}}{\mathrm{r}}\right]\\ \mathrm{P} . \mathrm{E} .=\left[\frac{\mathrm{e}^{2}}{4 \pi \varepsilon_{0} \mathrm{r}_{\mathrm{A}}}\right] \frac{\mathrm{r}_{\mathrm{A}}\left(\mathrm{r}_{\mathrm{b}}^{2}-3 \mathrm{R}^{2}\right)}{\mathrm{R}^{3}}\left[\text { multiplying by } \frac{\mathrm{r}_{\mathrm{A}}}{\mathrm{r}_{\mathrm{A}}}\right] \end{array}](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-54217743d4fb064afe627813fcad8439_l3.png)
From part (i), we have,
![]()
![Rendered by QuickLaTeX.com \therefore \mathrm{P} \cdot \mathrm{E}=27.2\left[\frac{0.53(\sqrt{530}-300)}{1000}\right]\left[\because \mathrm{r}_{\mathrm{b}}=(530)^{\frac{1}{4}} \mathrm{~A}^{\circ} \text { and } \mathrm{R}=10 \mathrm{~A}^{\circ}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-d169722f97bf64f45c9219a98e78abcd_l3.png)
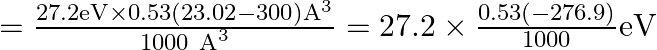
![]()
![]()
