![A=\left[\begin{array}{ll}3 & -4 \\ 1 & -1\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-16f776216ed4662f25a9fa186c592e2f_l3.png "Rendered by QuickLaTeX.com")
, show that 
is skew-symmetric.Solution:
We have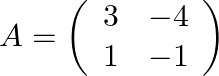 
The transpose of the matrix is an operation of making interchange of elements by the rule on positioned element 
shifted to new position 
The skew-symmetric matrix is defined as similarity of transpose of matrix with it self. i.e, 
.
(i) The transpose of 
are given by 
which can be written as
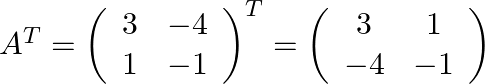
(ii) Next the subtraction of and can be processed as
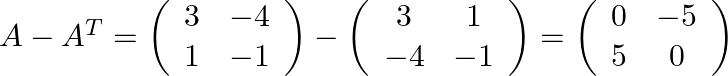
(iii) To check symmetric nature of 
as follow:
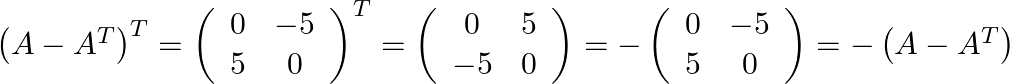
Thus it can be said that 
is skew-symmetric.